Lekcja 03 

CAD - Konstrukcje geometryczne

1. Wstęp
2. Ćwiczenie 1
3. Ćwiczenie 2
4. Ćwiczenie 3
5. Zadania

Wstęp
W czasach przed komputerowych, gdy rysunek techniczny polegał na rysowaniu na papierze z użyciem podstawowych przyrządów (ołówek, gumka, ekierka, linijka, cyrkiel), wykreślenie różnorodnych konstrukcji geometrycznych stanowiło czasami nie lada problem. Okrąg o zadanym promieniu styczny do dwóch innych, siedmiokąt foremny, obrót figury o zadany kąt, lustrzane odbicie, czy też banalne: proste równoległe, podział odcinka na połowy, dwusieczna kąta, środek okręgu itp. 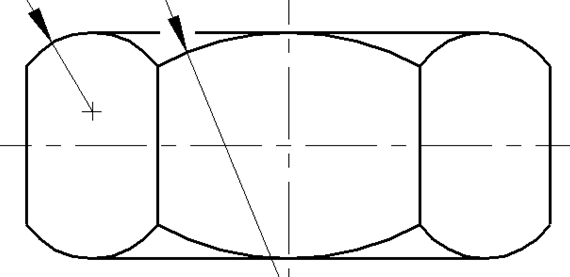Wyobraźmy sobie na przykład, że projektujemy uszczelkę pomiędzy elementami konstrukcji współczesnego samochodu przedstawioną na poniższym obrazku.

Wraz z nadejściem programów typu CAD, wszelkie tego typu zadania konstrukcyjne przejęły odpowiednie narzędzia zawarte w tych programach.

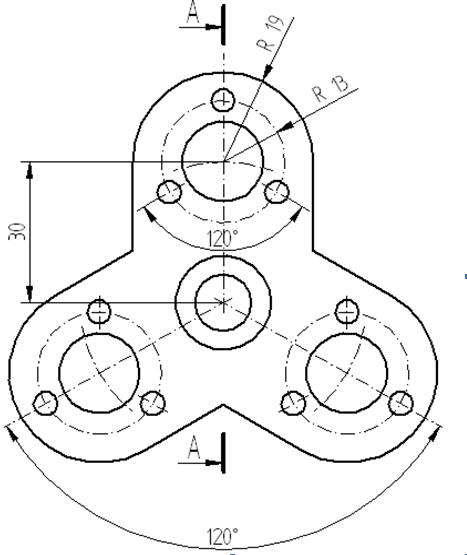
Ćwiczenie 1 - przycinanie, zaokrąglanie, obracanie

Narysuj część pokazaną na rysunku Sposobów rysowania jest tyle, ilu rysujących. Zaprezentowane rozwiązanie jest tylko jedną z propozycji.

Uwagi

• aby uaktywnić linię poleceń wciśnij CTRL+M,

• aby zatwierdzić wpisane w linii poleceń dane wciśnij ENTER

Okręgi

• Rysuj / Okrąg / Środek Punkt

• 0,0 ; 20

• 0,0 ; 60

• 0,0 ; 180

• 0,0 ; 200

Odcinki pod kątem

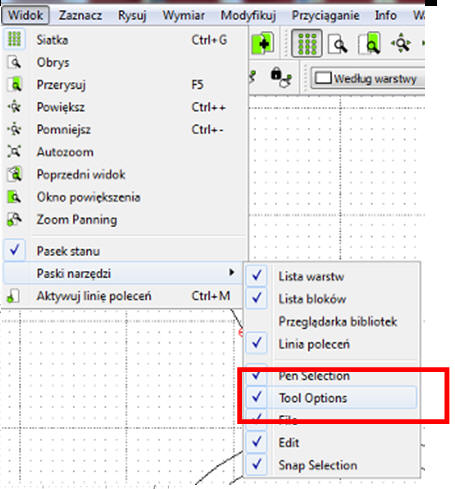
Sprawdzamy, czy widoczny jest pasek narzędzi, za pomocą, którego określimy dodatkowe parametry rysowanych obiektów

• Widok / Paski narzędzi / Tool Options

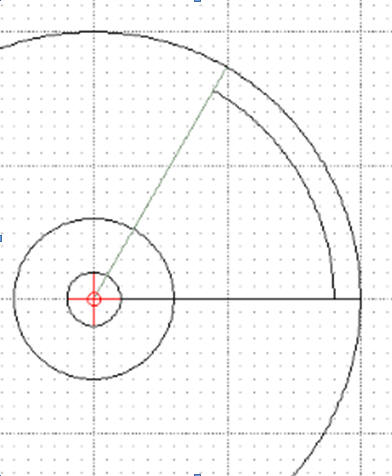
• Rysuj / Linia / Kąt

• Tool Option: Kąt: 0, Długość 200, Punkt przyciągania: Początek

• Linia poleceń wpisz początek: 0,0 pojawi się odcinek

• W podobny sposób umieść jeszcze jeden odcinek o początku w punkcie 0,0, kąt: 60, długość 200

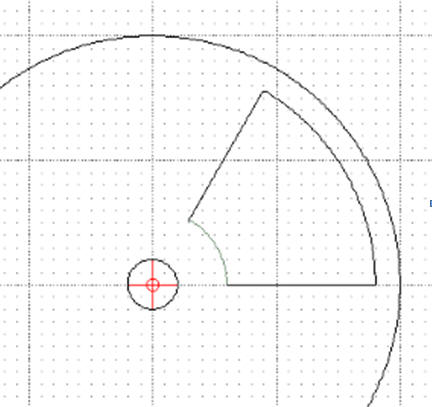
Usuwanie zbędnych krawędzi

• Modyfikuj / Przytnij

• Zaznaczamy obiekt ograniczający

• Zaznaczamy obiekt do przycięcia

Czerwone punkty pokazują miejsca na rysunku, w które należy kliknąć.

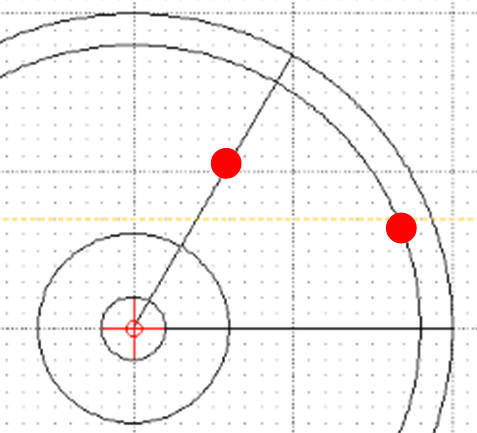
Bardzo ważna jest kolejność wskazywania obiektów! W podobny sposób usuwamy pozostałe krawędzie

Zaokrąglanie

Ostre przejścia pomiędzy fragmentami części maszynowych są z reguły zaokrąglane lub ścinane (fazowane)

• Modyfikuj / Zaokrąglaj

• Pasek narzędziowy Tool Options zaznacz Przytnij, wpisz Promień: 10

• Wskazujemy pierwszy obiekt

• Wskazujemy drugi obiekt

Czerwone punkty pokazują miejsca, w które należy kliknąć.

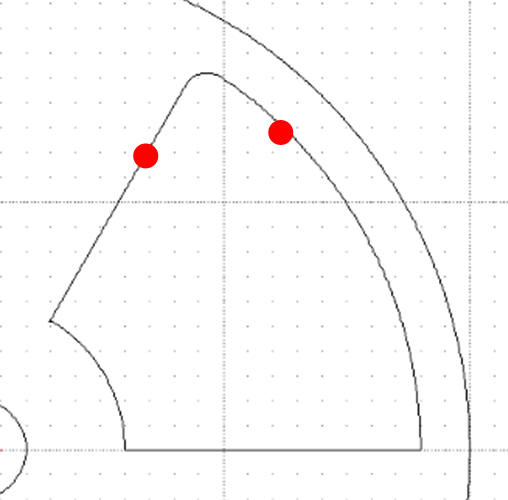
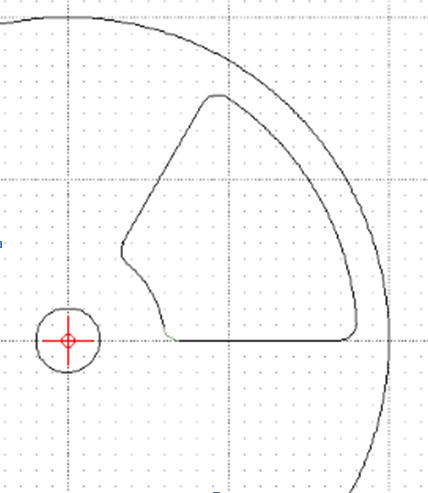
W podobny sposób zaokrąglamy pozostałe krawędzie. Uwaga - jeśli pojawiają się problemy podczas zaokrąglania brzegów, możesz spróbować usunąć je za pomocą przycinania

Kopiowanie przez obracanie

Zaokrąglony fragment skopiujemy jeszcze dwa razy poprzez obracanie, wokół punktu (0,0) z kątem 120°

• Zaznaczamy obiekt do skopiowania

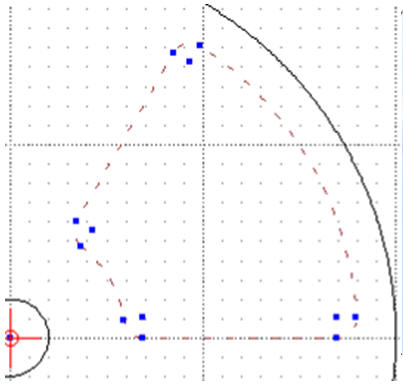
• Modyfikuj / Obracaj

• Zaznacz do obrócenia - wciskamy ENTER

• Środek obrotu - w linii poleceń wpisujemy: 0,0

• Punkt odniesienia - w linii poleceń wpisujemy: 0,0

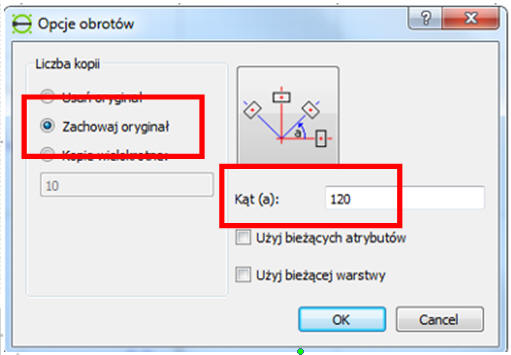
• Pojawia się okienko Opcje obrotów

• Wybieramy Zachowaj oryginał i wpisujemy kąt: 120

• W podobny sposób kopiujemy jeszcze raz obiekt

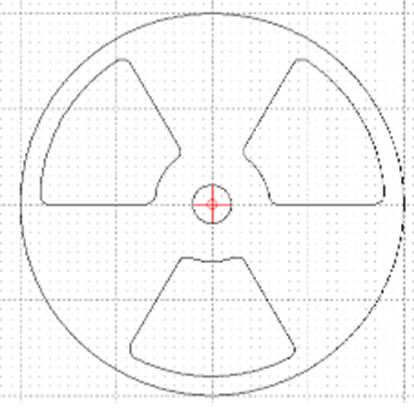
Zamiast wpisywać w linii poleceń punkt (0,0) dwa razy można kliknąć myszką w to miejsce. Aby wykonać to zadanie poprawnie należy bezwzględnie posłużyć się odpowiednim rodzajem przyciągania. UWAGA – na następnych lekcjach dowiesz się, w jaki sposób można kopiować wielokrotnie i automatycznie jakiś element. W AutoCad operacja ta nosi nazwę SZYK.

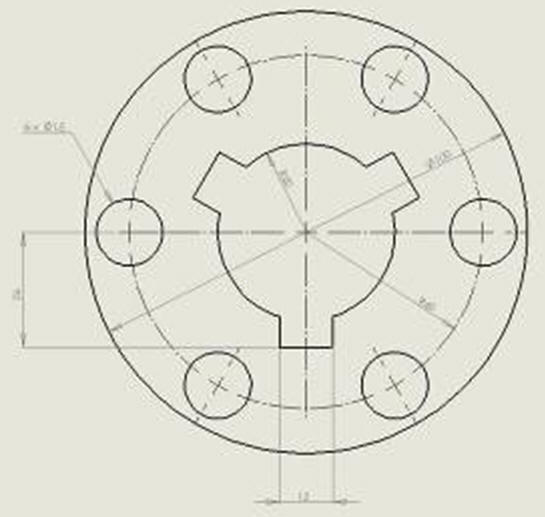
Ćwiczenie 2 - Linie pomocnicze. Styczne. Przycinanie

Narysuj część pokazaną na rysunku.

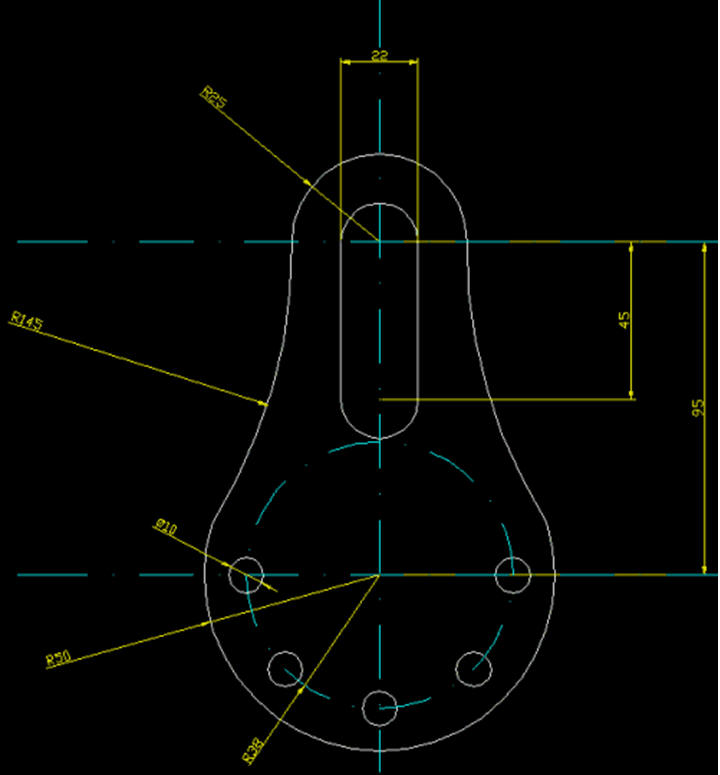
Przyjmujemy, że początek układu współrzędnych będzie w środku mniejszego, zewnętrznego koła - tam znajduje się linia bazowa podawanych wymiarów. Na osobnej warstwie wykreślimy linie pomocnicze - niebieski kolor

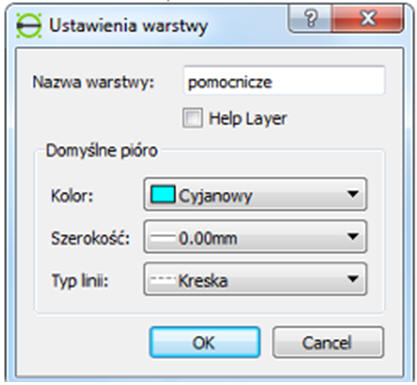
Warstwa i linie pomocnicze

• Warstwa / Dodaj warstwę

• Nazwa: POMOCNICZA, Kolor: niebieski, Typ linii: kreska

• Rysuj / Linia / Pionowy

• Pasek narzędzi Tool Options Długość: 250,

• Punkt przyciągania: Początek

• Linia poleceń: 0,-200

• Linia poleceń: 11,-200

• Linia poleceń: -11,-200

• Rysuj / Linia / Poziomy

• Pasek narzędzi Tool Options Długość: 200, Punkt przyciągania: Początek

• Linia poleceń: -100,0

• Linia poleceń: -100,11

• Linia poleceń: -100,25

• Linia poleceń: -100,-45

• Linia poleceń: -100,-56

• Linia poleceń: -100,-95

• Linia poleceń: -100,-145

• Rysuj / Okrąg / Środek Punkt

• Środek: 0,-95

• Promień: 38

• Blokujemy warstwę POMOCNICZA

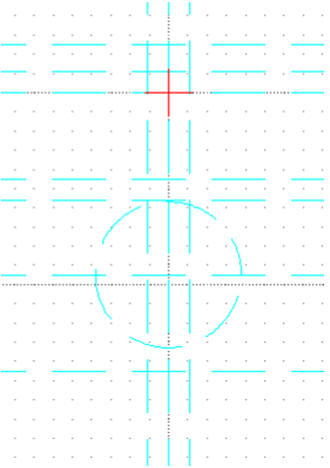
Okręgi

• Wybieramy warstwę 0

• Przyciąganie / Snap Intersection (do punktów przecięcia)

• Rysuj / Okrąg / Środek Punkt

• Środek - klikamy w punkt 0,0

• Promień - klikamy w punkt 0,11

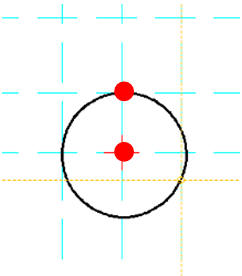
• W podobny sposób pozostałe okręgi

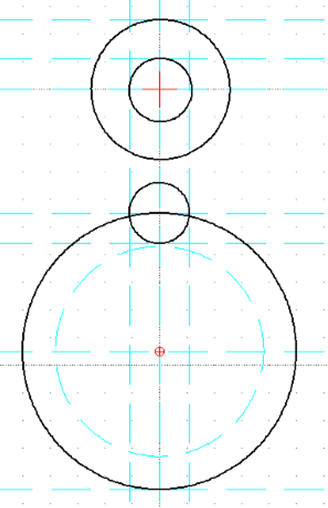
Ponieważ włączone przyciąganie do punktów przecięcia (pomocnicze niebieskie linie), dlatego wygodniej jest kliknąć myszką, niż wpisywać ręcznie w linii poleceń. Czerwone punkty pokazują miejsca, w które należy kliknąć, ważna jest kolejność! 

Odcinek styczny do dwóch okręgów

Konstruujemy odcinek styczny do dwóch okręgów. W naszym przypadku mamy zadanie ułatwione, gdyż oba małe okręgi są identyczne i leżą pionowo względem siebie, więc można po prostu ręcznie narysować te styczne odcinki. W ogólnym przypadku należy posługiwać się narzędziem zastosowanym poniżej.

• Odcinek / Rysuj / Styczna (C,C)

• Klikamy w pierwszy okrąg

• Klikamy w drugi okrąg Czerwone punkty pokazują miejsca na okręgach, w które należy kliknąć

• W podobny sposób drugi styczny odcinek

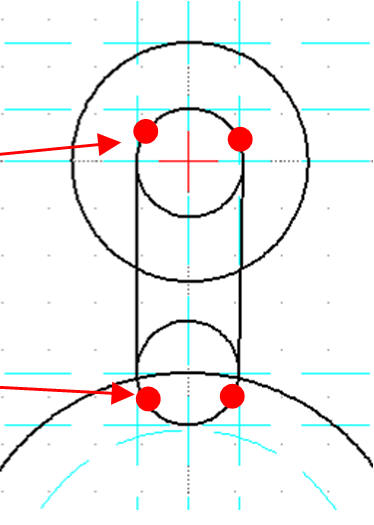
Okrąg styczny do dwóch okręgów

• Rysuj / Circle / Tangential 2 (styczny do dwóch okręgów)

• Pasek narzędzi Tool Option wpisz promień: 145

• Klikamy w pierwszy okrąg

• Klikamy w drugi okrąg

• Klikamy, aby zatwierdzić wybór okręgu

• W podobny sposób konstruujemy drugi okrąg styczny

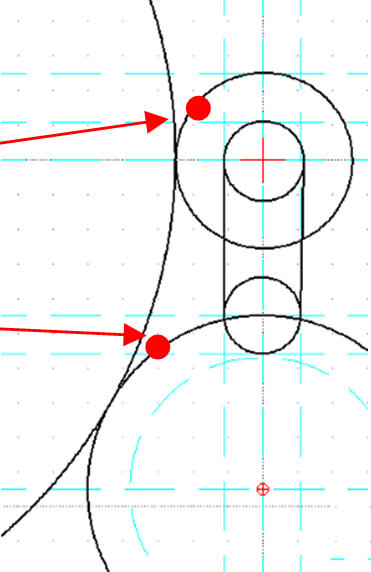
Czerwone punkty pokazują miejsca na okręgach, w które należy kliknąć

Usuwamy zbędne fragmenty

Korzystamy z narzędzia Przytnij lub dzielimy krzywe na fragmenty (Podziel) i usuwamy ręcznie

• Przyciąganie / Snap Intersection

• Modyfikuj / Podziel

• Obiekt do cięcia

• Punkt cięcia

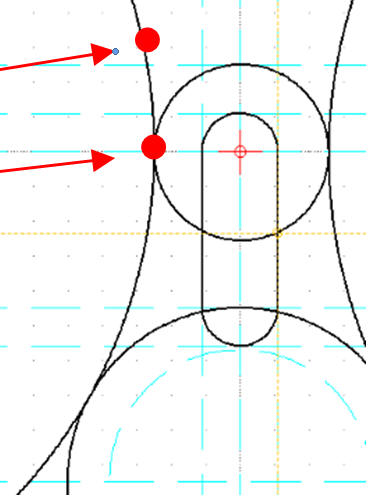
Ponieważ wybraliśmy przyciąganie do punktów przecięcia, dlatego nie mamy problemów z odnalezieniem właściwych miejsc. Czerwone punkty pokazują miejsca na okręgach, w które należy kliknąć, aby dokonać podziału. W pozostałych przypadkach postępujemy podobnie, a następnie usuwamy (zaznaczamy i DELETE).

Otwory

• Rysuj / Okrąg / Środek Punkt

• Klikamy w punkt pokazany na rysunku

• Aktywujemy linię poleceń - Promień: 5

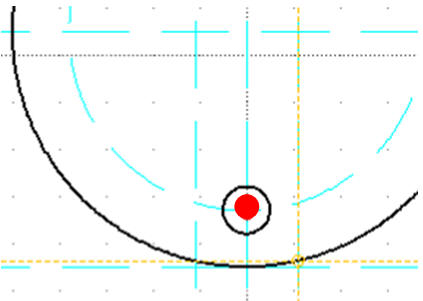
• Modyfikuj / Obracaj

• Zaznaczamy okrąg do obrócenia

• ENTER - koniec zaznaczania

• Klikamy w Punkt środkowy obrotu

• Klikamy w punkt odniesienia

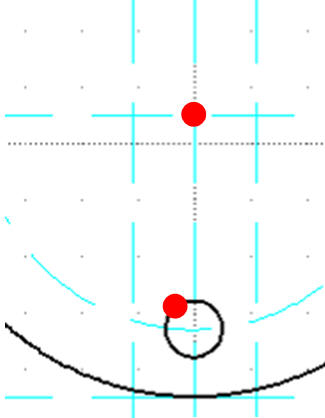
• W oknie Opcje obrotów wybieramy Zachowaj oryginał i kąt: 30

• W podobny sposób rysujemy pozostałe okręgi

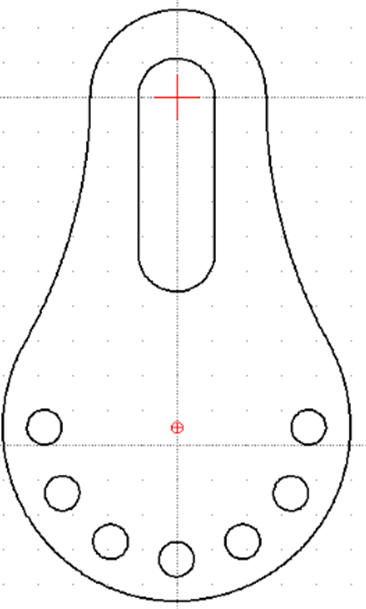
UWAGA – można wykorzystać również kopiowanie wielokrotne

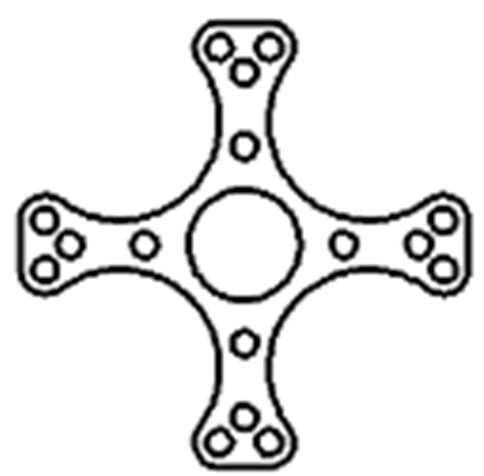
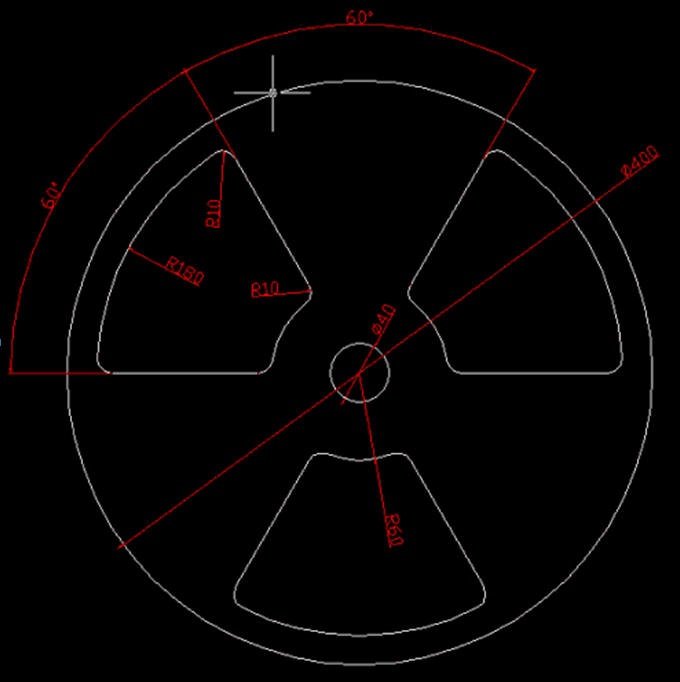
Ćwiczenie 3 - Styczne. Podział. Usuwanie

Narysuj część pokazaną na rysunku.

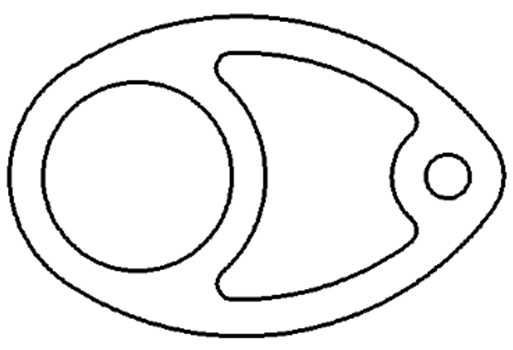
Wymiary dobierz samodzielnie. Całość składa się z różnej wielkości okręgów. Zbędne fragmenty będą usuwane poprzez podział: Modyfikuj / Podziel (można oczywiście zastosować przycinanie: Modyfikuj / Przytnij).Ponieważ wymiary nie są ważne, dlatego też technika rysowania może być nieco odmienna. Będziemy korzystać z przyciągania do siatki..

Okręgi

• Włączamy przyciąganie do siatki

• Okręgi: Punkt Środek

• Rysujemy dwie pary okręgów współśrodkowych

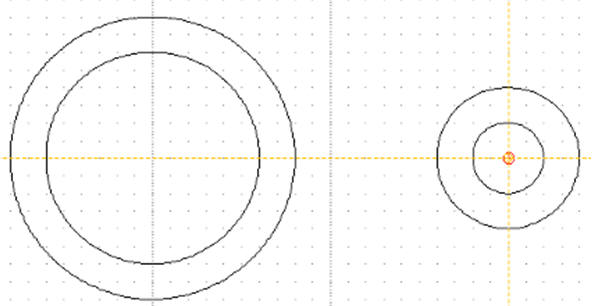
Styczne

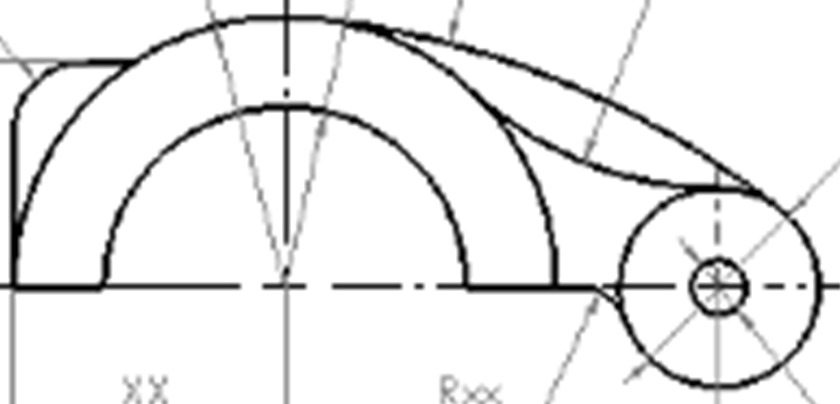
W poprzednim ćwiczeniu korzystaliśmy z możliwości konstruowania okręgu stycznego do dwóch innych - wersja wklęsła (Circle Tangential 2). Program LibreCAD w tej wersji niestety nie ma możliwości wykreślenia tym narzędziem okręgu w wersji wypukłej, dlatego też skorzystamy z innego narzędzia: Okręg z trzema punktami. Dodatkowo włączymy przyciąganie do linii obiektów.

• Włączamy przyciąganie do linii Przyciąganie / Snap On Entity

• Wyłączamy przyciąganie do siatki

• Rysuj / Okrąg / 3 Punkty

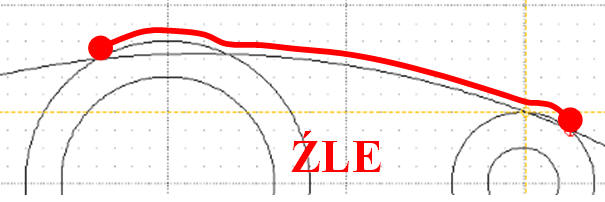
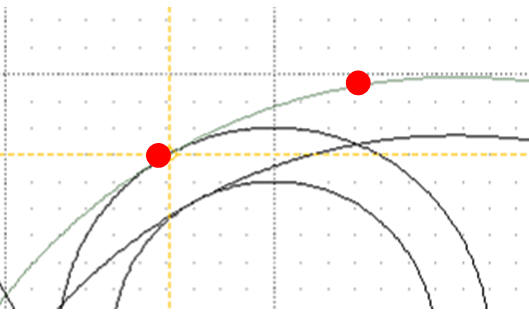
Gdy przesuwamy wskaźnik myszy porusza się jedynie po wykreślonych już liniach. Linia stycznego i wypukłego okręgu powinna łagodnie przechodzić w dwa okręgi ograniczające, dlatego też należy metodą „prób i błędów” tak dobrać punkty na okręgach, aby uzyskać wspomniany efekt. Na rysunkach pokazano niepoprawną i poprawną konstrukcję.

• Klikamy w punkt

• Klikamy w punkt

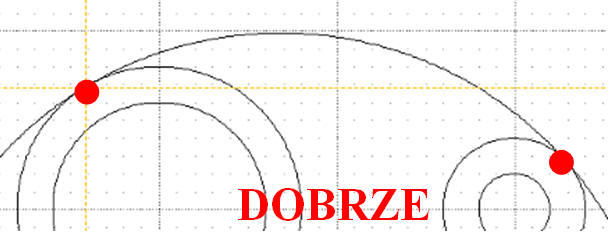
Rysunek obok pokazuje przykładowe usytuowanie tych punktów. Pojawia się okrąg styczny do tych punktów. Położenie trzeciego punktu dobieramy doświadczalnie tak, aby okrąg był styczny, wypukły i nastąpiło łagodne przejście.

• Klikamy w Punkt - dobieramy doświadczalnie

• W podobny sposób rysujemy pozostałe trzy styczne

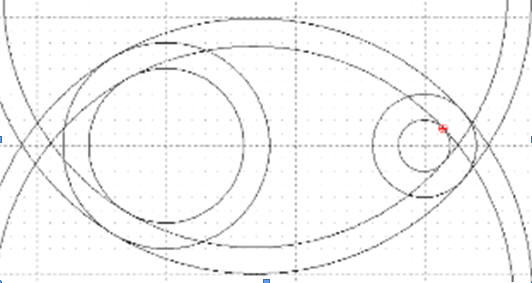
Podział i usuwanie

Aby sprawnie podzielić fragmenty okręgów na łuki wygodnie będzie posłużyć się przyciąganiem do punktów przecięcia - w innym przypadku będzie praktycznie niemożliwe trafienie w odpowiedni punkt.

• Włączamy przyciąganie do punktów przecięcia (Snap Intersection)

• Wyłączamy przyciąganie do Linii (On Entity)

• Modyfikuj Podziel

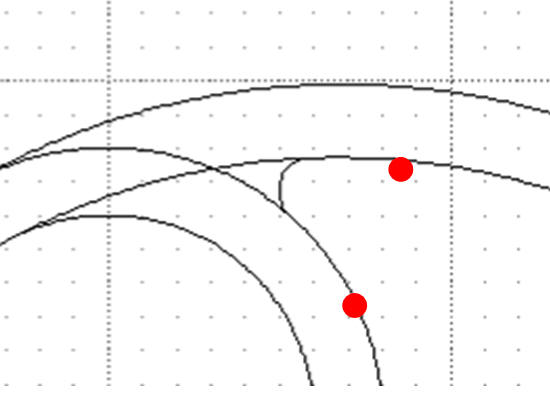
• Klikamy w okrąg

• Klikamy w punkt

Najpierw wskazujemy obiekt do cięcia (odpowiedni okrąg), a potem wybieramy punkt przecięcia - styczności. Jeden z przypadków pokazuje poniższy rysunek. Identyczną metodą należy posłużyć się w pozostałych siedmiu.

• Po podzieleniu wszystkich okręgów wybieramy wskaźnik wyboru (biała strzałka)

• Zaznaczamy odpowiedni łuk i wciskamy klawisz DELETE

Zaokrąglenia

Zaokrąglenia w środkowej części uzyskamy za pomocą kreślenia okręgów stycznych do dwóch innych (Circle Tangential 2). Wygodniej jednak posłużyć się narzędziem Zaokrąglaj.

• Modyfikuj / Zaokrąglaj

• Pasek narzędziowy Tool Options Promień: 10

Możemy również włączyć opcję Przytnij na tym pasku - program będzie automatycznie obcinał zbędne fragmenty. Nie zawsze jednak przycinanie działa poprawnie. Gdy opcja jest wyłączona, tylko rysujemy zaokrąglenie, a potem dokonujemy podziału i usunięcia zbędnych łuków.

• Klikamy w pierwszy okrąg

• Klikamy w drugi okrąg

• Klikamy, aby wybrać odpowiednie zaokrąglenie

• Identycznie w pozostałych przypadkach

• Dzielimy na fragmenty i usuwamy zbędne łuki

Zadania do samodzielnej realizacji