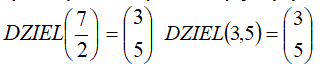mgr inż. Wacław Libront * Bobowa 2017-2019

ZSO Bobowa, ul. Długoszowskich 1, 38-350 Bobowa, tel: 0183514009, fax: 0183530221, email: sekretariat@zsobobowa.eu, www: zsobobowa.eu

Lekcja 2

Funkcje i zmienne

  1. Wstęp
  2. Stałe fizyczne
  3. Przypisanie-Wyliczenie
  4. Funkcje
  5. Definiowanie
  6. Zadania
  7. lekcja 2 - zmienne i stałe.sm

Wstęp

Kalkulatorowe obliczenia są proste, jeśli są nieskomplikowane i wykonujemy je jednorazowo. W praktyce bez wykorzystania zmiennych i stałych nie jest możliwe efektywne liczenie. Czym jest zmienna? Wyobraź sobie wirtualny pojemnik, który nazywamy w jakiś charakterystyczny sposób (np. „x”), do którego można wrzucić jakąś liczbę. W kolejnych rachunkach zamiast przepisywać tą liczbę wykorzystujemy nazwę pojemnika. W ten sposób zyskujemy bardzo sprawne narzędzie do wszelkiego rodzaju obliczeń. Jeśli korzystałeś kiedykolwiek z arkusza kalkulacyjnego, to jest to podobna sytuacja do zastosowania adresów komórek w formułach.

Podstawowe stałe fizyczne używane w programie

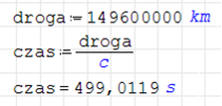
ĆWICZENIE 1 - prędkość światła

• Wpisz: droga : 149600000 ENTER
• Wpisz: czas : droga / c TAB ENTER
• Wpisz: czas = ENTER

UWAGA.
Zwróć uwagę na automatyczne wyliczenie jednostek. Zwróć uwagę na różne znaczenie znaku „:=” i „=”, Zwróć uwagę, że nie trzeba wpisywać obu znaków „:=” - wystarczy sam dwukropek, resztę uzupełnia komputer. Podobna sytuacja występuje przy nawiasach.
Program odszukuje zmienne od lewej do prawej i w dół (sposób naturalny). Oznacza to, że jeśli równanie, z którego korzysta zmienna znajdzie się bardziej po lewej lub wyżej tej zmiennej może nie zostać poprawnie wyliczone.

Przypisanie := Wyliczanie =

Ze znaku równości korzystaliśmy do tej pory, kiedy chcieliśmy coś wyliczyć, gdy program miał nam pokazać wynik obliczeń. Znak przypisania (dwukropek i znak równości bez odstępu) oznacza, że najpierw program wylicza wartość wyrażenia po prawej stronie, a wynik przypisuje do zmiennej po lewej stronie.

ĆWICZENIE 2 - równanie kwadratowe

Wylicz pierwiastki równania kwadratowego dla następujących parametrów równania: a=2, b=-3, c=1/2
Sposób obliczeń pokazuje rysunek po prawej stronie ekranu. Zwróć uwagę na obliczenia po prawej stronie; zamiast dwóch prawie identycznych wzorów zastosowano znak „±”.

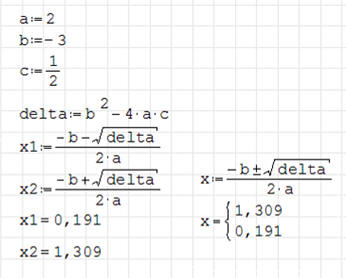
ĆWICZENIE 3 - wzory skróconego mnożenia

Udowodnij, że zachodzi równość pomiędzy wzorami: (a-b)2 i (a-b)(a+b)
oraz a2-2ab+b2.
Sposób obliczeń pokazuje rysunek po prawej stronie ekranu. Do zmiennych a i b można wpisywać różne wartości, po czym automatycznie zostaną wyliczone odpowiednie wzory - wszystkie dają takie same wyniki.

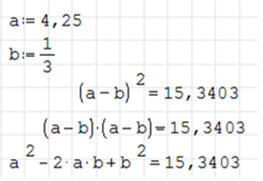
ĆWICZENIE 4 - oporniki

Zadanie z ćwiczeniami z lekcji 1 korzystając ze zmiennych

Zadanie rozwiązano dwoma sposobami
Aby uzyskać wynik w postaci ułamkowej naciśnięto klawisze CTRL „.”
Podczas wpisywania nazw zmienny z indeksami pamiętaj, aby po wpisaniu indeksu nacisnąć klawisz → (kursor w prawo), aby kolejne znaki były wpisywane bez indeksu. Bezpieczniej jednak nie posługiwać się indeksami lecz zwykłymi liczbami.

  

Funkcje

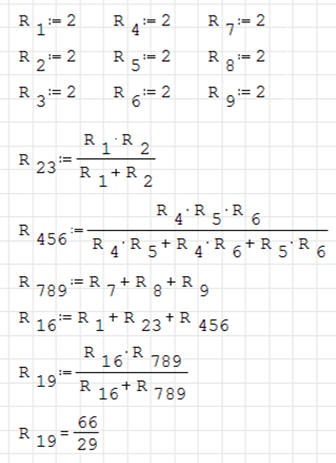
Program zawiera zestaw niezbędnych funkcji używanych w matematyce, które są wykorzystywane w wszelkiego rodzaju technicznych obliczeniach. Wstawiamy funkcje wybierając z menu: Wstaw / Funkcja lub wpisując bezpośrednio na kartce skróty. Użyteczne skróty funkcji wypisane są w poniższej tabeli

abs

 wartość bezwzględna

abs(-31) → 31

concat

 łączy łańcuchy tekstowe

concat("ala","ma","kota") → „alamakota”

cos

 cosinus

cos(30·deg) → 0,866

ctg

 cotangens

cos(30·deg) → 1,7321

exp

 funkcja ekspotencjalna (e do potęgi)

exp(1) → 2,7183

findstr

 szuka tekstu w innym tekście

findstr("alamakota";"k") → 6

mod

 reszta z dzielenia całkowitego

mod(10;3) → 1

num2str

 zamienia wyrażenie na tekst

num2str(1.5) → "3/2”

product

 iloczyn liczb

product(i;i;1;5) → 120 czyli 1*2*3*4*5

random

 liczba losowa

random(10) → liczby losowe od 0 do 9

range

 wektor kolumnowy

range(1;5) → 1..5

round

 zaokrąglenie liczby rzeczywistej

round(10/3;2) → 3,33

sin

 sinus

sin(30·deg) → 0,5

sqrt

 pierwiastek kwadratowy

sqrt(4) → 2

str2num

 zamienia tekst na liczbę

str2num(„2.5”) → 2,5

strlen

 liczba znaków w tekście

strlen(„alamakota”) → 9

substr

wycinanie tekstów

substr("alamakota",3;2)="am" od trzeciego dwa znaki

sum

 sumowanie elementów

sum(i/2;i;1;5) → 7,5 czyli 1/2+2/2+3/2+4/2+5/2

tg

 tangens

tg(30·deg) → 0,5774

trunc

 część całkowita liczby rzeczywistej

reunc (10/3) → 3

UWAGA - program rozróżnia duże i małe litery. X i x, to dwie różne zmienne.

ĆWICZENIE 6 - zasięg

Jak daleko poleci kamień wyrzucony pod kątem 30° z początkową prędkością 10 m/s.
Ponieważ kąt wpisano w stopniach, dlatego nie musimy zamieniać go na radiany, aby funkcja sinus poprawnie go zinterpretowała.

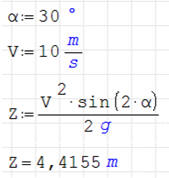
ĆWICZENIE 7 - ciągi liczbowe

Sprawdź czy dla n=100 zachodzi poniższa równość:


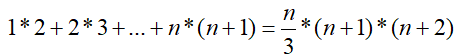
to matematyczny symbol oznaczający sumowanie liczb. W naszym zadaniu sumujemy elementy podanego wzoru dla zmiennej n, od 1 do 100, co 1. Czyli dla n=1 otrzymamy n•(n+1)=2, dla n=2 otrzymamy 6, dla n=3 mamy 12 itd.

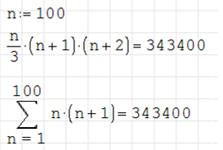
ĆWICZENIE 8 - operacje na tekstach

W zmiennej znajduje się nazwisko i imię rozdzielone spacją (np. „Libront Wacław”). Rozdziel ten napis na dwa osobne zawierające nazwisko i imię (np. „Libront”, „Wacław”).

Definiowanie nowej funkcji

Jeżeli mamy zamiar wiele razy wykorzystywać te same skomplikowane wyrażenia w swoich obliczeniach (np. omawiany już zasięg w rzucie ukośnym), to wygodniej byłoby zdefiniować swoją własną funkcję, do której „wrzucimy” niezbędne dane, i która będzie potrafiła ten zasięg wyliczyć. Oczywiście w programie mamy taką możliwość, co pokazano na poniższych przykładach. Dodatkowo funkcje takie będą automatycznie przeliczały jednostki.

ĆWICZENIE 9 - zasięg

Zdefiniuj funkcję, która dla zadanych parametrów prędkości początkowej i kąta wyliczy zasięg w rzucie ukośnym. Wylicz zasięg w kilometrach
Zdefiniowano funkcję ZAS z dwoma parametrami. Po wstawieniu konkretnych wartości, wynik podawany jest w metrach. Można zamienić na kilometry - wynik zostanie automatycznie przeliczony

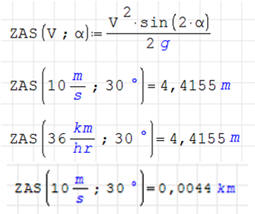
ĆWICZENIE 10 - ciągi liczbowe

Zdefiniuj funkcję, która wyliczy sumę N wyrazów następującego ciągu:


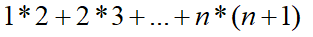
Podczas definiowania parametrów funkcji wbudowanej SUM, program automatycznie wyświetla matematyczny znaczek sumowania i można wpisywać parametry do odpowiednich komórek. Poniżej zestaw znaków, które należy wpisać:
• Wpisz: ciąg(N → : sum TAB i * ( i + 1 → → → ; i ; 1 ; N ENTER
• Wpisz: ciąg ( 100 = ENTER

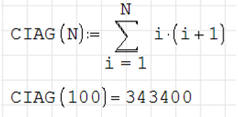
Instrukcja LINE i UKŁAD RÓWNAŃ

Definiowanie bardziej złożonych funkcji wymaga zastosowania dwóch dodatkowych poleceń programu. Pierwsze z nich LINE pozwala połączyć kilka pojedynczych instrukcji w jeden ciąg - blok instrukcji.
W programowaniu mówi się w tym wypadku o procedurach. W ćwiczeniu 8 wyodrębnialiśmy z łańcucha tekstowego napis przed spacją i napis za spacją. Aby tego dokonać konieczne było wyliczenie położenia spacji i wyliczenie długości łańcucha. Samo zaś wyodrębnianie też wymagało użycia odpowiednich funkcji. Te wszystkie operacje można oczywiście wykonywać na naszej wirtualnej kartce, ale jeśli chcemy „nauczyć” program robić to „za jednym zamachem” należałoby je wszystkie wstawić, co prowadzi do produkowania ogromnych wyrażeń.


Możemy też zastosować instrukcję LINE i połączyć je w jedną całość bez konieczności wstawiania. Instrukcja LINE jest dostępna na pasku Programowanie lub w menu: Wstaw / Funkcja / Programowanie / Line. Instrukcja Line wyświetla standardowo tylko dwie linie. Aby zwiększyć ich ilość należy ustawić kursor tekstowy na końcu bloku, aż pojawi się czarny kwadracik w prawym dolnym rogu (jak pokazano na rysunku obok) - wtedy można myszką przeciągnąć w dół i utworzyć dodatkowe pola.

 

Drugie polecenie UKŁAD RÓWNAŃ służy do tworzenia bloków, które grupują wyniki obliczeń.
Z jej pomocą możemy np. „nauczyć” funkcje, aby podawała wiele rozwiązań. Spotykamy taki przypadek w znanym ogólnie równaniu kwadratowym, które posiada dwa rozwiązania (!). Instrukcja dostępna jest na panelu Funkcje

ĆWICZENIE 11 - operacje na tekstach

Utwórz funkcję, która rozdzieli nazwisko i mię w jednym napisie na dwa osobne wyrazy bez spacji.

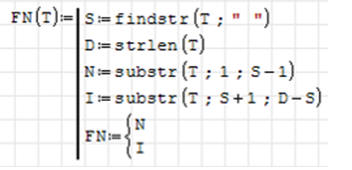
• Za pomocą funkcji FINDSTR szukamy spacji rozdzielającej wyrazy
• Funkcja STRLEN podaje liczbę znaków w łańcuchy tekstowym
• Do zmiennej N wycinamy S-1 znaków począwszy od pierwszego - pierwszy wyraz
• Do zmiennej I wycinamy D-S znaków począwszy od S+1 - drugi wyraz
• Obie zmienne przypisujemy do nazwy funkcji w bloku grupującym dwa wyniki

Przykłady zastosowania funkcji pokazują poniższe rysunki

Za pomocą indeksowania możemy otrzymać pojedynczy element z bloku wyników.
Jeżeli jako parametr funkcji podamy np. jeden wyraz, to nie będzie możliwe „wyliczenie” wyrazów.

ZADANIA

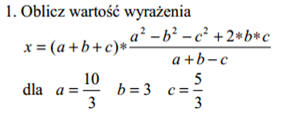
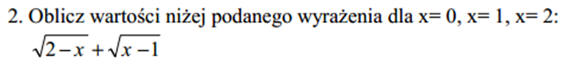
3. Utwórz funkcję o nazwie PIERWIASTKI, która dla parametrów: a, b, c obliczy oba pierwiastki równania kwadratowego. Funkcja ma zwracać oba pierwiastki jednocześnie.

4. Utwórz następujące funkcje i sprawdź poprawność obliczeń


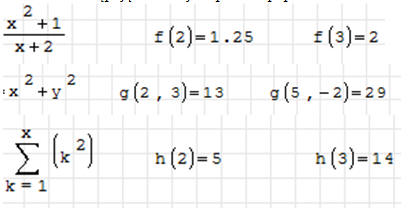
5. Za pomocą funkcji SUBSTR napisz nową funkcję o nazwie LEWY, która będzie wycinać określoną w parametrze liczbę znaków z lewej strony. Przykład: LEWY(„Wacek”;3) = „Wac”

6. Za pomocą funkcji SUBSTR napisz nową funkcję o nazwie PRAWY, która będzie wycinać określoną w parametrze liczbę znaków z lewej strony. Przykład: LEWY(„Wacek”;3) = „cek”

7. Za pomocą funkcji SUBSTR napisz nową funkcję o nazwie INIC, która wytnie pierwsze litery wyrazów. Przykład: INIC(„Wacław Libront”) = „WL”

8. Za pomocą funkcji NUM2STR i SUBSTR napisz nową funkcję DZIEL, która z podanej liczby rzeczywistej wycina część całkowitą i ułamkową i podaje, jako wynik. Przykład: