Lekcja 3

Wykresy

1. Wstęp
2. Obiekty
3. Wykresy 3D
4. Zadania
5. lekcja 3 - wykres i obiekty.sm
6. lekcja 3 - wykresy.sm

Wstęp

Graficzna prezentacja wyników obliczeń, czy też przebiegu jakiejś funkcji ma duże znaczenie w naukowych obliczeniach. Choć konkretny wynik obliczeń jest najważniejszy dla inżyniera, to możliwość zobrazowania całego zakresu, czy też zorientowania się w tendencji ma również niebagatelne znaczenie. Programy CAS bez problemu potrafią generować wykresy dwu i trójwymiarowe.

ĆWICZENIE 1 - funkcja kwadratowa

Zobrazuj na wykresie przebieg funkcji kwadratowej o parametrach: a=1/2, b=3, c=-5.
• Wstaw / Wykres / 2D (lub znak „@”)
• Wpisz: 1 / 2 →, x ^ 2 → + 3 * x - 5 ENTER

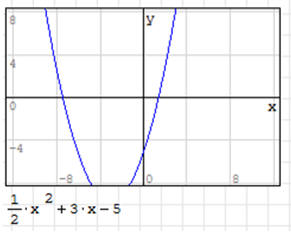
Pojawi się wykres pokazany na obrazku obok. Jeżeli klikniemy we wnętrze wykresu - pojawią się „kwadraciki” - będziemy mogli za pomocą myszki zmieniać wymiary wykresu, przesuwać go wewnątrz obszaru oraz skalować: SHIFT+kółko - oś X, CTRL+kółko - oś Y, ALT+kółko lub samo kółko- oś X i Y

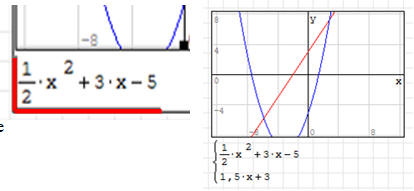
ĆWICZENIE 2 - funkcja liniowa

Na wykresie z poprzedniego ćwiczenia umieść wykres drugiej funkcji: y=1.5x+3
• Ustaw kursor na początku równania - patrz czerwona linia na obrazku
• Wstaw instrukcję układu równań - panel Funkcje
• Wpisz: 1,5 * x + 5 ENTER

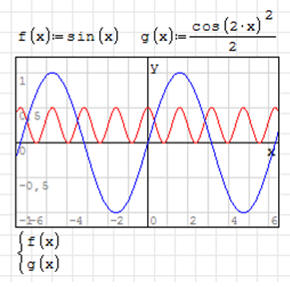
ĆWICZENIE 3 - funkcje trygonometryczne

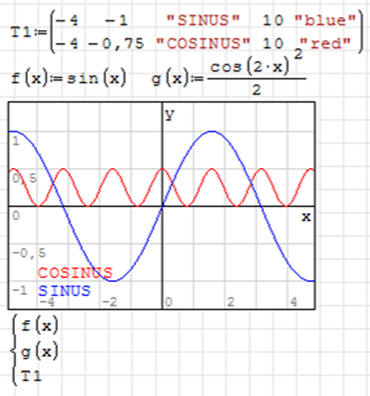
Umieść na jednym wykresie funkcje: f(x)=sin(x) oraz g(x)=cos2(2x)/2
Aby umieścić dwie lub więcej funkcji na wykresie należy użyć bloku równań.

ĆWICZENIE 4 - teksty na wykresie

Umieść na wykresie teksty opisujące funkcje:
„SINUS” i „COSINUS”
W obszarze wykresu możemy umieszczać dowolne informacje, w szczególności dotyczy to tekstów, choć z powodzeniem można wstawiać dowolne obiekty graficzne, a nawet animować wykresy. Definicja takiego obiektu składa się z pięciu elementów umieszczonych w poziomej tablicy. Jeśli w jednej definicji chcemy umieścić kilka napisów używamy większej tablicy, np. 2x5.
• Wpisz: T : CTRL+M
• Wpisz w okienku wiersze: 2, kolumny 5, ENTER
• Wpisz: -4 → → -1 → → SINUS → → 10 → → blue ENTER

Obiekty na wykresie

Definicja każdego obiektu na wykresie składa się z pięciu elementów umieszczonych w poziomym wektorze (macierzy, tablicy). Kolejne pola wektora definiują współrzędną X, współrzędną Y, napis, wielkość i kolor. Aby zdefiniować większą ilość obiektów w jednej zmiennej korzystamy z tablicy, która ma więcej wierszy i 5 kolumn. Tworzenie tablicy wywołujemy za pomocą kombinacji klawiszy CTRL+M lub z menu Wstaw / Macierz.

Koła. Okręgi. Krzyże

Standardowo wyświetlane są litery i cyfry w odpowiednich miejscach. Dla znaków „.”, „o” i „x” znaleziono jednak też inne zastosowanie.

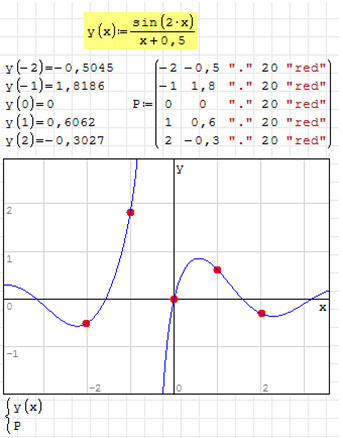
ĆWICZENIE 5 - punkty na wykresie

Narysuj wykres funkcji .
Dla odciętych: -2, -1, 0, 1, 2 wylicz rzędne i narysuj niebieski punkty o wielkości 20 na krzywej.
Do wzoru wstawiamy wartości odciętych i w ten sposób otrzymujemy rzędne dla punktów
Tworzymy tablicę 5x5 i wpisujemy do niej odpowiedni wartości
Do wykresu dodajemy nowy obiekt za pomocą bloku równań

Wykresy 3D

Na osi X odkładamy odcięte funkcji f(x). Na osi Y odkładamy odcięte funkcji f(y). Oś Z zawiera rzędne obu wykresów. Przesuwanie i skalowanie odbywa się nie za pomocą opisanych już przy wykresach 2D kombinacji klawiszy, lecz za pomocą palety Wykres.

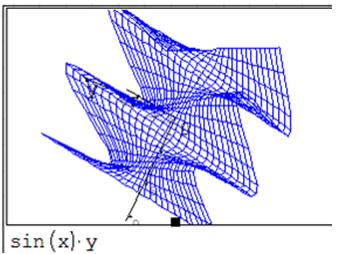
ĆWICZENIE 6 - funkcja sin(x)*y

Narysuj wykres 3D funkcji sin(x)*y

ĆWICZENIE 7 - 2 funkcje

Na jednym wykresie 3D narysuj funkcje:

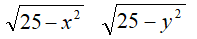
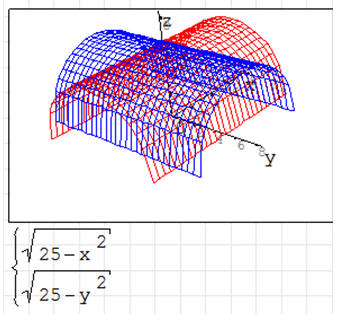
ĆWICZENIE 8 - punkty przecięcia

Znajdź pierwiastki i punkty wspólne krzywej 5x2-3 i prostej 2x+2 z dokładnością do 3 miejsc po przecinku metodą graficzną miejsca

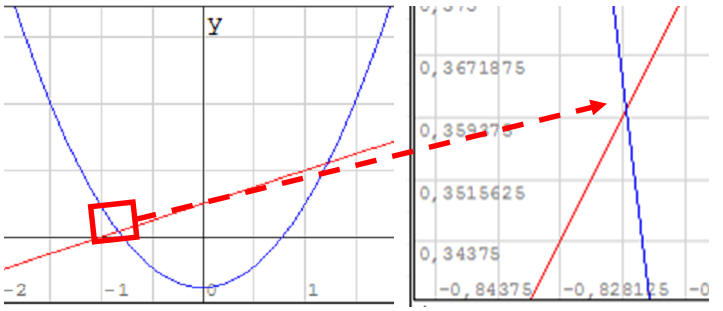
Za pomocą skalowania i przesuwania doprowadzamy do sytuacji, gdzie na wykresie możemy z dużą dokładnością stwierdzić, jakie są współrzędne. W sytuacji pokazanej na rysunku współrzędna Y wynosi 0,359 z dokładnością do 3 miejsc po przecinku. Współrzędnej X nie możemy dokładnie podać. Możemy dalej skalować lub spróbować uśrednić wyniki z obu stron (-0,8281+ -0,8125)/2 daje wynik -0,8203. Opisujemy punkt przecięcia, jako (-0,820; 0,359).

Narysuj miejsca zerowe w postaci kolorowych punktów o wielkości 20.
Narysuj punkty przecięcia w postaci kolorowych okręgów o wielkości 20.
Po wyznaczeniu wszystkich współrzędnych tworzymy obiekt tablicowy 5x5 i wypełniamy odpowiednimi wartościami.
Zamiast jednej tablicy można również utworzyć trzy oddzielnie na każdy rodzaj punktów

ZADANIA

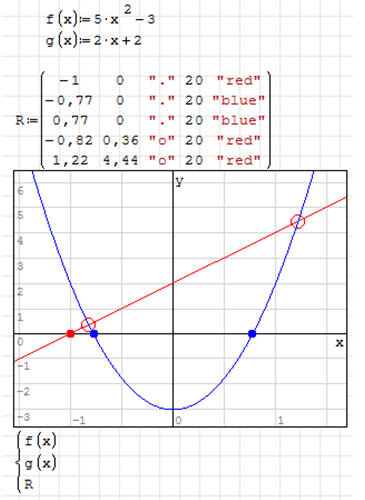
Utwórz wykresy, znajdź miejsca zerowe i punkty przecięcia się krzywych metodą wykreślną korzystając z możliwości skalowania wykresu z dokładnością do 3 miejsc po przecinku.
W znalezionych punktach ustaw kolorowe kropki o wielkości 20.
f(x)=x•sin(x)-4 f(x)=2x3-4x2+3x-1
g(x)=9 g(x)=-4x2+12x-2