mgr inż. Wacław Libront * Bobowa 2017-2019

ZSO Bobowa, ul. Długoszowskich 1, 38-350 Bobowa, tel: 0183514009, fax: 0183530221, email: sekretariat@zsobobowa.eu, www: zsobobowa.eu
mgr inż. Wacław Libront * Bobowa 2017-2019

ZSO Bobowa, ul. Długoszowskich 1, 38-350 Bobowa, tel: 0183514009, fax: 0183530221, email: sekretariat@zsobobowa.eu, www: zsobobowa.eu
Czym jest macierz? Z praktycznego punktu widzenia, to tabela
(wiersze i kolumny), w komórkach której zapisano jakieś liczby. Jeżeli tabela ma
jedną kolumnę lub jeden wiersz mówimy raczej - wektor. Matematycy potrafią
wykonywać na macierzach bardzo ciekawe działania, które służą do rozwiązywania
wielu skomplikowanych zadań. Dla naszych potrzeb wystarczy informacja, że przy
pomocy macierzy można w prosty sposób rozwiązywać układy równań liniowych.
Trzy równania z trzema niewiadomymi i mnóstwo żmudnych, papierowych obliczeń.
Nikt tego nie lubi. Co trzeba zrobić, żeby równania algebraiczne sprowadzić do
postaci macierzowej i rozwiązać szybko przy użyciu programu komputerowego?
Mamy dane dwa równania liniowe:
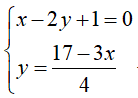
Po pierwsze trzeba je uporządkować
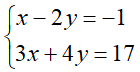
Po drugie konstruujemy dwie macierze
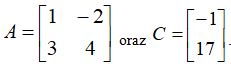
Po trzecie trzeba napisać w programie „invert(A)•C=”
I to by było na tyle - program sam poda rozwiązanie. Tajemnicza funkcja INVERT
„tworzy macierz odwrotną. Na szczęście nie musimy umieć konstruować macierzy
odwrotnej. Robi to za nas program.
ĆWICZENIE 1 - układ równań
Rozwiąż układ równań liniowych .
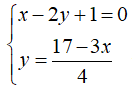
Sprawdź otrzymany wynik.
• Wpisz: A: CTRL+M
• Wpisz do okna Wstawianie macierzy Wiersze: 2 i Kolumny: 2, ENTER

• Wypełnij pustą macierz liczbami: 1 → -2 → → 3 → 4 ENTER
• Wpisz C: CTRL+M
• Wpisz do okna Wstawianie macierzy Wiersze: 2 i Kolumny: 1, ENTER
• Wypełnij pustą macierz liczbami: -1 → → 17 ENTER
• Wpisz: invert(A → *C ENTER
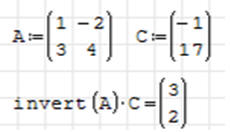
Otrzymujemy wynik. Zgodnie z początkowymi ustawieniami w
pierwszym elemencie znajduje się szukana wartość zmiennej x, a w drugiej -
wartość zmiennej y. Nazwy macierzy mogą być dowolne.
• Rozwiązanie x=3 oraz y=2
Sprawdzenia otrzymanych wyników
Możemy wykonać dwoma sposobami"
• porównujemy ze sobą obie strony jednego z równań - wynik 1 (PRAWDA) gdy jest
poprawnie
• przenosimy prawą stronę na lewą - wynik 0, gdy jest poprawnie
Sprawdzimy na wszelki wypadek oba równania
• Wpisz: 3 - 2 * 2 + 1
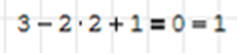
• Wstaw / Operator / Logiczne RÓWNY =
Logiczne „=” nie jest tym samym, czym „=” pokaż wynik
• Wpisz: 0 = ENTER
Powinniśmy otrzymać w wyniku 1 (logiczne PRAWDA), co oznacza poprawność
rozwiązania. Logiczne 0 (FAŁSZ) oznacza błąd w obliczeniach. A teraz drugi
sposób - najpierw należy przenieść wszystkie wyrazy na jedną stronę, prawa
strona równa 0. Sprawdzenia dokonamy na drugim równaniu
• Wpisz: 2 - ( 17 - 3 * 3 → → → / 4 = ENTER
Powinniśmy otrzymać w wyniku 0, czyli prawą stronę równania.
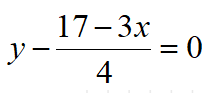
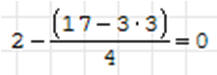
ĆWICZENIE 2 - układ trzech równań liniowych
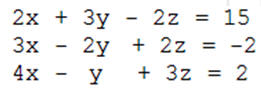
Rozwiąż układ równań liniowych pokazanych na rysunku
Rozwiązujemy w podobny sposób, jak opisano powyżej.
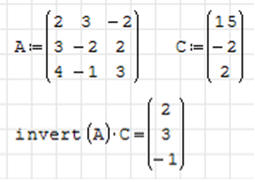
• Rozwiązanie: x=2, y=3, z=-1
• Sprawdzenie:
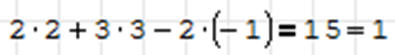
ĆWICZENIE 3 - suma dwóch liczb
Suma dwóch liczb wynosi 32, a ich różnica -4. Znajdź te
liczby.
• Tworzymy dwa równania: x+y=32 oraz x-y=-4
• Tworzymy macierze i rozwiązujemy według znanego schematu.
• Sprawdzenie: 14 + 18 - 15 = 0
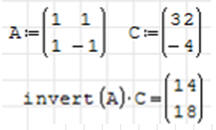
ĆWICZENIE 4 - klasy sportowe
W klasach IIa i IIb było razem 57 uczniów. W zawodach
sportowych wzięło udział 80% uczniów kl. IIa i 75% uczniów kl. IIb, co stanowiło
razem 44 uczniów. Ilu uczniów liczyła każda z tych klas?
• Konstruujemy układ równań
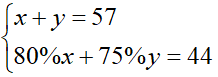
• Tworzymy macierze i rozwiązujemy
Graficzne rozwiązanie - oba równania mają swoje odzwierciedlenie na wykresie, a rozwiązanie układu równań i znalezienie X i Y, to nic innego, jak punkt przecięcia się dwóch krzywych.
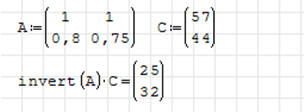
ĆWICZENIE 5 - Rozwiąż poprzednie zadanie graficznie.
• Układ równań zapisujemy w postaci funkcyjnej:
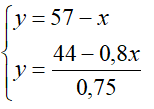
• Tworzymy wykres z dwoma funkcjami: y1 i y2
mogą być inne oznaczenia, np. y(x), f(x)
• Punkt przecięcia się funkcji jest rozwiązaniem układu (narysowano obiekt)
obiekt na wykresie tworzymy jako wektor o jednym wierszu i pięciu kolumnach (x,
y, znak, wielkość, kolor)
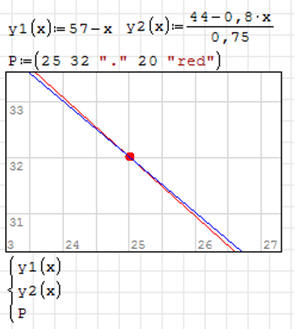
Funkcja RANGE - wektor (lista) wypełniony liczbami
Funkcja RANGE tworzy tablicę jednowymiarową i automatycznie
wypełnia je liczbami.
Listy możemy dodawać lub odejmować od siebie lub mnożyć lub dzielić przez
liczbę.
ĆWICZENIE 6 - liczby naturalne
Utwórz wektor z pięcioma pierwszymi liczbami naturalnymi
• Wpisz: range TAB
Pojawia się pole zakresu z możliwością wpisania dwóch liczb: startowej i
końcowej
• Wpisz: 1 → 5 ENTER
Pojawia się zapis: „1..5”. Jeżeli chcemy zobaczyć bardziej przyjazną postać
należy użyć znaku równości.
W nawiasach pionowo uporządkowane liczby naturalne od 1 do 5.
• Wpisz: range TAB 1 → 5= ENTER
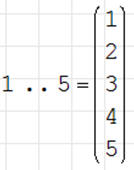


ĆWICZENIE 7 - liczby parzyste
Utwórz wektor, która zawierać będzie pięć pierwszych liczb
parzystych
• Wpisz: range TAB 1 → 5 → * 2 = ENTER
Kursor powinien obejmować cały wektor a nie jego fragment! Jeżeli pomnożymy
tylko drugą liczbę przez 5 (a nie cały zakres) otrzymamy listę liczb naturalnych
1..20!

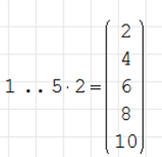

Inny sposób. Funkcja RANGE pozwala zdefiniować pierwszy i
drugi element, a następne będzie tworzyć na podstawie ich różnicy.
• Wpisz: range TAB 2 ; 10 → 4 → = ENTER
Liczby do funkcji wpisujemy „nie po kolei”, choć można ustawiać kursor ręcznie.
Pierwszym elementem jest liczba 2. Drugim elementem jest liczba 4, Kolejne
elementy (aż do 10) będą tworzone automatycznie na podstawie różnicy pierwszych
dwóch - różnica dodawana do ostatniego.

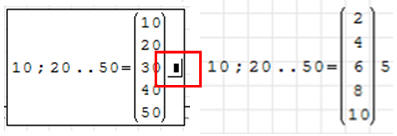
Jeszcze inny sposób. Wykorzystanie dzielenia całego zakresu
• Wpisz: range TAB 10 ; 50 → 20 = → → 5 ENTER
Przez chwilę pojawia się wektor z kolejnymi dziesiątkami.Za wektorem znajduje
się pole, za pomocą którego dzielimy wszystkie liczby wektora przez wpisaną
liczbę (czerwone pole)
ĆWICZENIE 8 - radiany
Utwórz wektor, w którym otrzymasz kolejne wartości kątów w
stopniach:
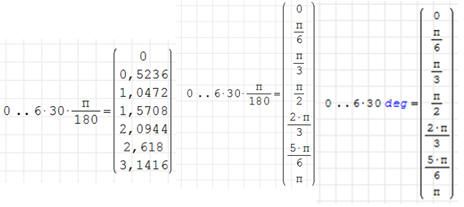
0, 30, 60, …, do 180 w postaci radianów.
Kolejne obrazki pokazują wykonywane działania: wartości kątów w stopniach,
zamiana na radiany i obliczenie wartości funkcji
• Wpisujemy zakres 0..6 i mnożymy wektor przez 30
• Mnożymy przez π i dzielimy przez 180
Jeśli wciśniemy CTRL+”.” - pojawi się wynik w postaci ułamkowej.
ĆWICZENIE 9 - prędkość
Oblicz, z jaką prędkością jedzie samochód, jeżeli w ciągu
jednej sekundy pokonuje odcinek drogi równy 10 metrów. Wykonaj podobne
obliczenia dla kolejnych odcinków: 20, 30, 40, 50 metrów. Wyniki zaprezentuj w
postaci wektora. Prędkość samochodu podaj w kilometrach na godzinę.
Obliczenia możemy przeprowadzić bez wprowadzania jednostek i sami musimy martwić
się o przeliczanie. Możemy też od razu podczas definiowania zmiennych opisać je
za pomocą jednostek i nastąpi automatyczne przeliczenie. Oba sposoby pokazano na
rysunkach. Dodatkowo będziemy mieli możliwość przeliczania na inne jednostki,
np. m/s na km/hr.
• Wpisz: prędkość =
Otrzymamy wektor z liczbami.
Aby nastąpiło automatyczne przeliczenie na jednostki należy wpisać:
• Wpisz: prędkość = → km TAB / hr TAB ENTER


ĆWICZENIE 10 - listy
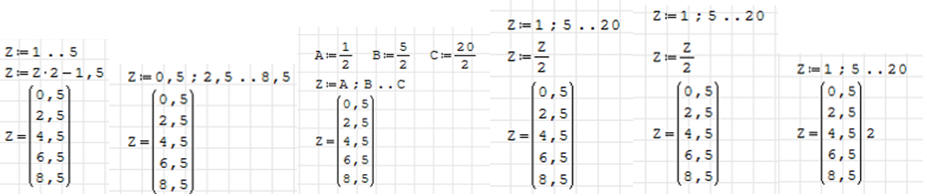
Za pomocą funkcji RANGE utwórz listę o nazwie Z wypełnioną
następującymi liczbami: 0,5 2,5 4,5 6,5 8,5
Rysunki pokazują kilka możliwości utworzenia takiej listy
Za 5 zeszytów i 2 ołówki zapłacono 8,20 zł, a za 8 takich samych zeszytów i 3 takie same ołówki zapłacono 13 zł. Jaka jest cena zeszytu?
Obwód prostokąta wynosi 60 cm. Jeśli krótszy bok tego prostokąta zwiększymy o 3 cm, a dłuższy skrócimy o 3 cm, to otrzymamy kwadrat. Oblicz pole tego prostokąta.
Bażanty i króliki miały razem 35 głów i 98 nóg. Ile było bażantów a ile królików?
Za każde bezbłędnie rozwiązane zadanie uczeń otrzymuje 10 punktów, ale za każde źle rozwiązane zadanie traci 5 punktów. Po rozwiązaniu 20 zadań uczeń otrzymał 80 punktów. Ile zadań rozwiązał dobrze, a ile źle?
Suma cyfr pewnej liczby dwucyfrowej wynosi 12. Jeśli do tej liczby dodamy 18, to otrzymamy liczbę utworzoną z tych samych cyfr, ale napisanych w odwrotnej kolejności. Jaka to liczba?
W dwóch skrzynkach były 54 cytryny. Gdy z jednej skrzynki przełożono do drugiej 9 cytryn, wówczas okazało się, że w obu skrzynkach znalazło się tyle samo. Ile cytryn było w każdej skrzynce na początku?
W przepisie na surówkę stosunek ilości marchewki do ilości kapusty wynosi 3:8. Ile kg kapusty, a ile marchewki trzeba przygotować, aby zrobić 22 porcje tej surówki po 15 dag każda?
Na łące pasą się owce i gęsi. Razem jest ich 40. Ile jest owiec, a ile gęsi, jeżeli łączna suma ich kończyn wynosi 110?
W słoiku znajdowało się 350 cukierków - kukułek i irysów. Zostało zjedzonych 25% irysów i ani jedna kukułka i okazało się, że kukułek jest tyle samo co irysów. Ile cukierków każdego rodzaju, było na początku w słoiku?
Test składał się z 20 pytań. Uczeń odpowiedział na wszystkie pytania. Za każdą prawidłową odpowiedź otrzymał dwa punkty, a za każdą błędną stracił jeden punkt. Ostatecznie uczeń otrzymał 16 punktów. Ilu poprawnych, a ilu błędnych odpowiedzi udzielił uczeń?
W pokoju znajduje się 105 figurek kryształowych,
porcelanowych i drewnianych. Figurek drewnianych jest dwa razy więcej niż
porcelanowych. Figurek kryształowych jest o 15 więcej od wszystkich pozostałych
figurek. Ile figurek każdego rodzaju znajduje się w pokoju?
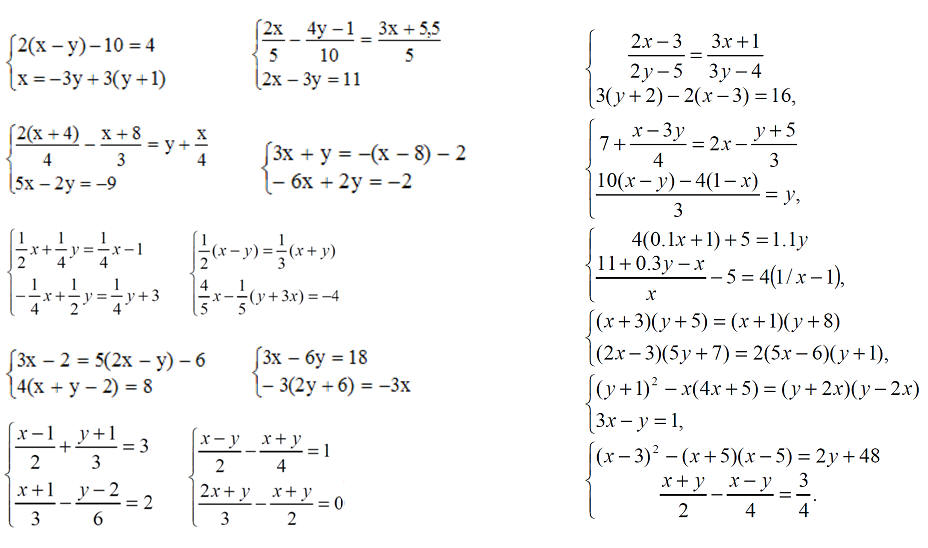
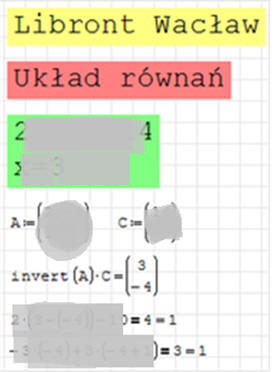
UKŁAD RÓWNAŃ
Rozwiąż układ równań liniowych 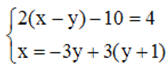
Kolejność czynności:
jeśli masz problem, to przeczytaj początek lekcji 4 i ćwiczenie 1
1. Wstaw region tekstowy w kolorze żółtym
i napisz w nim swoje nazwisko i imię
2. Wstaw region tekstowy w kolorze czerwonym
i napisz w nim „Układ równań”
3. Uporządkuj równania, tzn. doprowadź oba do postaci Ax+By=C
Wstaw region tekstowy w kolorze zielonym
i napisz w nim oba uporządkowane równania
4. Przygotuj macierz o wymiarach 2x2 o nazwie A
i wpisz do niej współczynniki „stojące” przy x i y
macierz wywołujemy za pomocą skrótu CTRL+M
5. Przygotuj macierz o wymiarach 2x1 o nazwie C
i wpisz do niej współczynniki „wolne”
6. Wylicz wyrażenie invert(A)•C
otrzymasz nową macierz, w której znajdują się poszukiwane x i y
7. Sprawdź otrzymane wyniki wstawiając wyliczone x i y do równań
Posłuż się sposobem opisanym pod ćwiczeniem 1: Sprawdzenie…
znak porównania (logiczne =) wstaw za pomocą CTRL=
ZADANIE TEKSTOWE
Za 5 zeszytów i 2 ołówki zapłacono 8,20 zł, a za 8 takich samych zeszytów i 3
takie same ołówki zapłacono 13 zł. Jaka jest cena zeszytu?
Kolejność czynności:
jeśli masz problem, to przeczytaj ćwiczenia 3, 4 i 5
1. Wstaw region tekstowy w kolorze czerwonym
i napisz w nim „Zadanie tekstowe”
2. Ułóż równania do zadania (uporządkowane)
i wpisz je w region tekstowy w kolorze zielonym
3. Przygotuj dwie macierze dla tego układu równań
4. Znajdź rozwiązanie układu za pomocą wyrażenia invert(A)•C
5. Sprawdź otrzymane wyniki wstawiając je do równań
6. Zapisz oba równania w postaci funkcji, np. Y1(x) i Y2(x)
7. Narysuj na wspólnym wykresie te dwie funkcje
8. Narysuj punkt przecięcia w kolorze czerwonym o wielkości 20
Zauważ, że otrzymany za pomocą polecenia INVERT wynik powinien być taki sam, jak
część wspólna oby funkcji

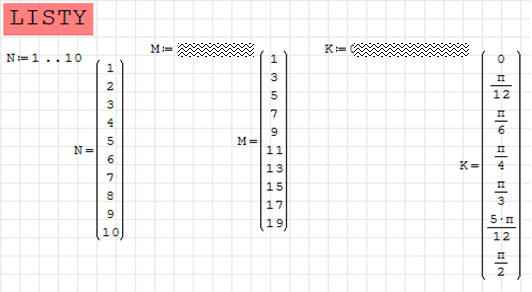
LISTY
Listy i zakresy:
Kolejność czynności:
jeśli masz problem, to przeczytaj ćwiczenia 6-10
1. Utwórz zmienną o nazwie „N” w której znajdą się kolejne liczby naturalne od 1
do 10
2. Wyświetl na ekranie zawartość tej zmiennej
3. Utwórz zmienną o nazwie „M” w której znajdą się kolejne liczby nieparzyste od
1 do 19
4. Wyświetl na ekranie zawartość tej zmiennej
5. Utwórz zmienną o nazwie „K” w której znajdą się kolejne wartości kątów od 0
do 90 co 15 stopni
6. Wyświetl na ekranie zawartość tej zmiennej w radianach