Lekcja 5

Układy równań algebraicznych

1. Wstęp
2. Funkcja Solve
3. Błędy obliczeń
4. Funkcja PolyRoots
5. Zadania
6. SAMODZIELNIE
7. lekcja 5 - pierwiastki.sm

Wstęp

Na poprzednich lekcjach zajmowaliśmy się m.in. wyliczaniem pierwiastków równania kwadratowego. Tak się składa, że znane są różne sposoby, aby te pierwiastki (czyli miejsca przecięcia się wykresu z osią X) wyliczyć. Jeszcze prościej można znaleźć miejsce przecięcia się równania liniowego z osią X. Jednak większość funkcji nie ma tak łatwych rozwiązań i czasami trzeba posiłkować się bardzo skomplikowanymi i pracochłonnymi metodami. Z pomocą oczywiście przychodzą komputery, które bez problemu tworzą wykresy i liczą z prawie dowolną dokładnością miejsca zerowe. Programy CAS również posiadają możliwości automatycznego wyznaczania pierwiastków równań. Służy do tego dwie funkcje SOLVE i POLYROOTS.

SOLVE(funkcja; zmienna) - szukanie pierwiastków równania lub układu równań
Otrzymujemy jedno lub więcej rozwiązań (wektor) w zakresie określonym przez ustawienia programu: Narzędzia / Ustawienia / Obliczenia / Pierwiastki. Standardowo od -20 do 20
SOLVE(funkcja; zmienna; od; do)
Ręcznie określamy zakres poszukiwań rozwiązań w podanym zakresie

ĆWICZENIE 1 - pierwiastki - funkcja SOLVE

Wylicz pierwiastki równania kwadratowego, dla następujących parametrów równania: a=2, b=-3, c=1/2. Posłuż się funkcją SOLVE. Sprawdź poprawność rozwiązania.
W tym przypadku całość sprowadza się do odpowiedniego zapisania danych dla funkcji. Na rysunkach obok pokazano cztery sposoby. 1- równanie kwadratowe zapisano bezpośrednio do funkcji, 2-najpierw zdefiniowano funkcję f(x), którą wstawiono do funkcji SOLVE, 3- wyniki zapisano w osobnej zmiennej wektorowej, 4-użyto porównania logicznego z wartością zero.

Sprawdzamy poprawność poprzez wstawienie wyników do funkcji - powinny wyjść wartości zerowe (lub bliskie zerowych – niedokładność obliczeń numerycznych)

UWAGA – odwołanie do komórki wektora (macierzy) poprzez indeks
W trzecim sposobie rozwiązania równania zdefiniowano zmienną X, która zawiera od razu oba rozwiązania – program automatycznie tworzy ze zwyczajnej zmiennej wektor (tablica o dwóch komórkach). Aby „wyciągnąć” pojedyncze rozwiązanie odwołujemy się poprzez indeks (naciskamy klawisz „[” - lewy nawias kwadratowy).

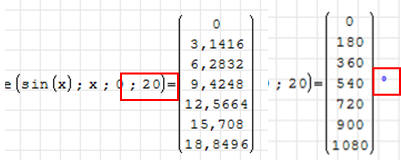
ĆWICZENIE 2 - pierwiastki sin(x)

Znajdź miejsca przecięcia się funkcji sin(x) z osią X w zakresie (0..20).
Obok przedstawiono dwa rozwiązania: w standardowym zakresie (-20..20) i w zakresie ustawionym ręcznie (0..20). Jeżeli chcemy otrzymać rozwiązanie w stopniach należy wstawić znak „°” w odpowiednim miejscu lub pomnożyć wynik przez „deg” - nastąpi automatyczna konwersja radianów na stopnie.

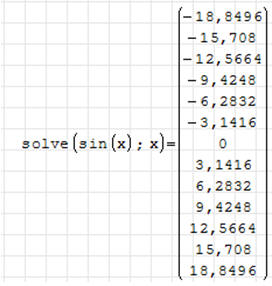
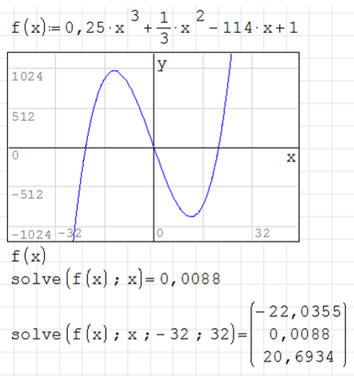
ĆWICZENIE 3 - pierwiastki wielomianu

Znajdź pierwiastki wielomianu:
Aby znaleźć wszystkie trzy pierwiastki najlepiej najpierw narysować wykres, aby zorientować się w zakresie poszukiwań, gdyż standardowy (-20..20) może być niewystarczający. Wpisanie zbyt dużego zakresu może znacznie wydłużyć czas obliczeń lub spowodować błędne obliczenia!

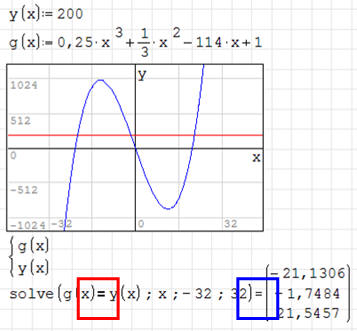
ĆWICZENIE 4 - punkty przecięcia

Znajdź punkty przecięcia się krzywej wielomianu z ćwiczenia 3 z prostą przecinającą oś Y w punkcie 200.
• Definiujemy funkcję y(x)=200
• Dodajemy funkcję do wykresu za pomocą symbolu „Układ równań”
• Za pomocą funkcji SOLVE przyrównujemy obie. Używamy operatora logicznego „=” z palety Logika.
Logiczne „=” nie jest tym samym, czym zwyczajne „=” wpisywane z klawiatury. Logiczne służy do porównywania i wynikiem jest prawda lub fałsz, a zwyczajne służy do wyświetlania wyników. Czerwona ramka logiczne „=”, niebieska ramka - zwykłe.
• Rozwiązanie: P1(-21.1306, 200), P2(-1.7484, 200), P1(21.5457, 200)
można też posłużyć się czwartym sposobem z ćwiczenia 1: solve(g(x)=200;x)

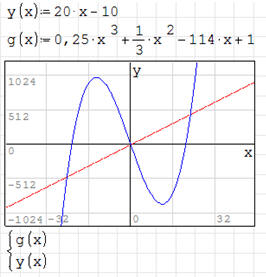
ĆWICZENIE 5 - punkty przecięcia - rzędne

Znajdź punkty przecięcia się krzywych wielomianu z ćwiczenia 4 i krzywej określonej równaniem y=20x-10.
Rozwiązanie zostało pokazana na rysunkach.
• Wykres z dwoma krzywymi
• Funkcja SOLVE przyrównuje obie krzywe i otrzymujemy wartości odciętych w zmiennej Z
• Wstawiamy odcięte do jednej z funkcji, aby otrzymać rzędne punktów wspólnych
Zwróć uwagę, że wartości rzędnych możemy obliczać pojedynczo wpisując, jako parametr funkcji Y lub G - posługujemy się w takim przypadku indeksem (np. Z1, Z2, itd.).

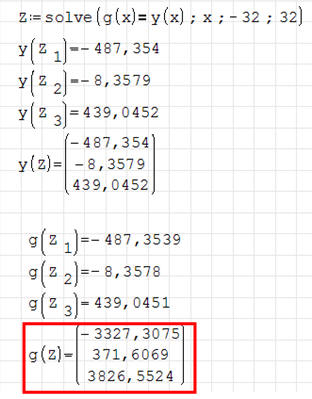
Możemy też otrzymać wektor z wynikami, wpisując po prostu zmienną Z, jako parametr.
Zwróć uwagę, że próba rozwiązania za pomocą g(Z) kończy się niepowodzeniem - otrzymujemy błędne wyniki. Dlatego bardzo ważne jest sprawdzanie rozwiązań, czy to graficznie, czy też podstawiając pojedyncze wyniki do równania (czerwona ramka).

Dokładność obliczeń. Błędy w obliczeniach.

Jak każdy program komputerowy, tak też i narzędzia CAS „liczą niedokładnie”. Co to oznacza? Komputer nie może zapamiętać liczb z dowolnie dużą dokładnością. Z reguły kilkanaście pierwszych liczb po przecinku. W zupełności wystarcza to do większości inżynierskich zastosowań. Trzeba jednak mieć świadomość, że obliczenia wykonywane są według jakiegoś algorytmu. Na przykład szukanie miejsc zerowych polega na wielokrotnym podstawianiu coraz dokładniejszych wartości, aż osiągniemy oczekiwaną wartość. Taki sposób pracy powoduje czasem powstawanie „dziwnych” błędów, dlatego trzeba mieć tego pełną świadomość i zawsze sprawdzać otrzymane wyniki.
Wróćmy do ćwiczenia 1, w którym obliczyliśmy pierwiastki równania kwadratowego. Jeżeli takie wyniki wstawimy do wzoru funkcyjnego powinniśmy otrzymać zero, bo to jest miejsce zerowe. Okazuje się jednak, że w obu przypadkach po podstawieniu wychodzi liczba bardzo bliska zeru, ale nie zero!

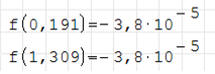
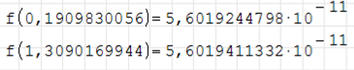
Standardowo program ustawiony jest na pokazywanie pierwszych czterech liczb po przecinku. Możemy zwiększyć dokładność obliczeń wybierając z menu: Narzędzia / Ustawienia / Obliczenia / Liczba cyfr po przecinku. Zwiększenie dokładności do 10 cyfr po przecinku spowoduje dokładniejsze obliczenia (ale też nie zero)!

ĆWICZENIE 6 - rozwiąż równanie

Rozwiąż równanie: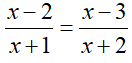
Doprowadzamy równanie do postaci „funkcyjnej”:
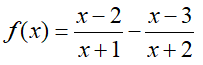
i wstawiamy, jako parametr funkcji SOLVE. Zwróćmy uwagę, że nie musi to być postać czystego wielomianu.

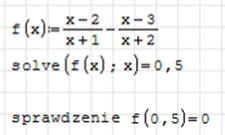
Funkcja POLYROOTS - szukanie pierwiastków wielomianu

Jako parametr funkcji podajemy wektor wypełniony uporządkowanymi współczynnikami wielomianu. jako rozwiązanie otrzymujemy wektor z pierwiastkami. Należy pamiętać o kolejności podawanych współczynników. Jeżeli wielomian nie ma współczynnika z odpowiednią potęgą, to wpisujemy 0.

ĆWICZENIE 7 - pierwiastki wielomianu

Znajdź pierwiastki wielomianu: 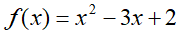i sprawdź poprawność obliczeń.
Używamy funkcji POLYROOTS, której podajemy wektor złożony ze współczynników wielomianu. Zwróć uwagę na kolejność współczynników w wektorze - największa potęga na końcu wektora.

Aby sprawdzić poprawność musimy pierwiastki wstawić do zmiennej (tutaj wektor X).
Sprawdzamy po kolei każdy pierwiastek (używając indeksowania) - w tej wersji programu nie mamy możliwości wstawienia do funkcji (jako parametr) wektora!

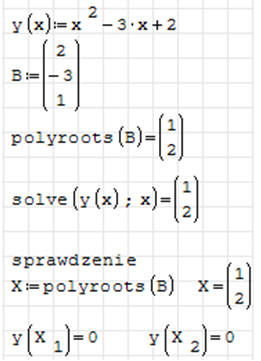
ĆWICZENIE 8 - pierwiastki wielomianu

Znajdź pierwiastki wielomianu:
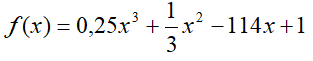
Sprawdź poprawność obliczeń. Znajdź miejsce przecięcia z osią OY. Narysuj wykres funkcji. Umieść charakterystyczne punkty na wykresie.

ZADANIA

1. Znajdź metodą graficzną oraz za pomocą funkcji SOLVE punkty wspólne krzywej określonej równaniem x•sin(x)-4 oraz prostej przechodzącej przez punkt 9 na osi Y i równoległej do osi X , w przedziale (0..16).

2. Znajdź pierwiastki poniższych wielomianów za pomocą funkcji SOLVE i POLYROOTS

SAMODZIELNIE

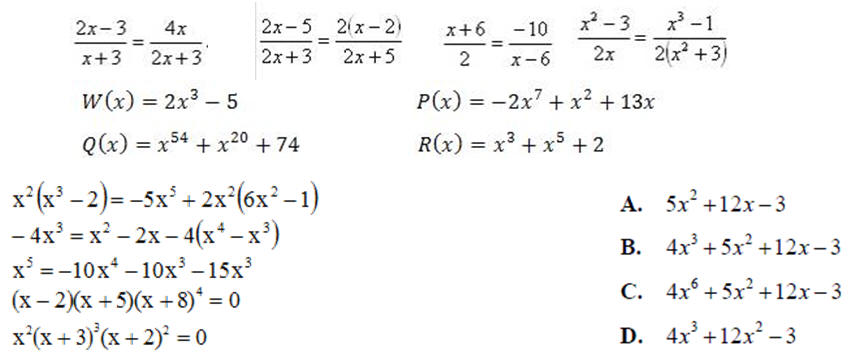
Pierwiastki (a ogólnie punkty wspólne) wyznaczamy na matematyce rozwiązując układy równań. Programy typu CAS wyliczają je numerycznie – służą do tego funkcje SOLVE i POLYROOTS

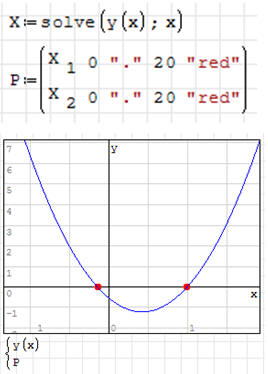
ZADANIE 1
Znajdź pierwiastki równania kwadratowego

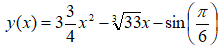
jeżeli masz problem przeczytaj ćwiczenie 1
* znajdź pierwiastki czterema sposobami
1) do funkcji SOLVE wstawiamy równanie w postaci ax2+bx+c
2) do funkcji SOLVE wstawiamy opis funkcji w postaci y(x)
3) wynik funkcji SOLVE wstawiamy do zmiennej
4) do funkcji SOLVE wstawiamy wyrażenie logiczne, której wynikiem jest część wspólna obu funkcji
* sprawdź poprawność jednego z rozwiązań dwoma sposobami
* narysuj wykres funkcji y(x)
* na wykresie narysuj dwa punkty w kolorze czerwonym w miejscach zerowych; wartości współrzędnych miejsc zerowych wpisz nie liczbowo lecz za pomocą indeksów – patrz rysunek
UWAGA - zwróć uwagę, że pierwiastki otrzymane za pomocą funkcji SOLVE powinny być zgodne z punktem przecięcia obu krzywych na wykresie

ZADANIE 2
Znajdź punkty przecięcia krzywych opisanych równaniami:

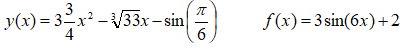
jeżeli masz problem przeczytaj ćwiczenie 4 i 5

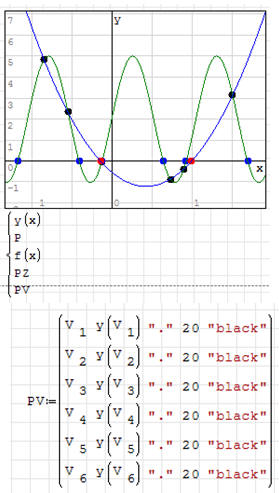
* znajdź pierwiastki funkcji f(x) dowolnym sposobem w przedziale <-2, 2>
(8 wartości)
* sprawdź poprawność rozwiązań – dla wszystkich 8 punktów
* wstaw funkcję do wykresu z poprzedniego zadania
* na wykresie narysuj miejsca zerowe funkcji f(x) w kolorze niebieskim (przedział <-2, 2>)
* znajdź miejsca przecięcia funkcji y(x) i f(x) (6 punktów)
* wstaw na wykres punkty przecięcia się obu funkcji w kolorze czarnym
do wyznaczenia punktów posłuż się indeksami – rysunek obok
zmienna V zawiera wartości rzędnych punktów wspólnych
UWAGA – gdyby znaleźć punkty wspólne obu krzywych metodami algebraicznymi, to powinny być takie same, jak pierwiastki otrzymane za pomocą funkcji SOLVE i powinny być zgodne z punktami przecięcia obu krzywych na wykresie.

ZADANIE 3
Do znalezienia miejsc zerowych wielomianu y(x) użyj funkcji POLYROOTS
jeżeli masz problem przeczytaj ćwiczenie 7 i 8