Lekcja 6

Optymalizacja. Pochodna funkcji

1. Wstęp
2. Pochodna
3. Optymalizacja
4. Zadania
5. SAMODZIELNIE
6. lekcja 6 - optymalizacja.sm

Wstęp

Optymalizacja jest działaniem, którego zadaniem jest znalezienie jak najlepszego rozwiązania. Z matematycznego punktu widzenia chodzi z reguły o odnalezienie maksimum lub minimum jakiejś funkcji. W innych dziedzinach będziemy mieli do czynienia np. z maksymalizacją zysków przy minimalizacji kosztów (finanse), maksymalizacją wydajności przy minimalizacji zużycia paliwa (procesy produkcyjne), maksymalizacją wytrzymałości przy minimalizacji zużycia materiałów konstrukcyjnych (budownictwo), minimalizacja czasu pracy, mocy i wykorzystania zasobów komputera przy maksymalizacji osiąganych wyników (informatyka), itd. Ponieważ jednak wszystkie te nauki są ściśle określone i większość procesów opisana za pomocą równań matematycznych, dlatego też większość przypadków odnosi się do matematycznego wyszukiwania maksimum lub minimum (tzw. ekstrema funkcji).

Pochodna

W analizie matematycznej mówi o szybkości zmian jakiejś funkcji. Jeżeli zaś wyliczymy pochodną funkcji i przyrównamy ją do zera, to pierwiastki tego równania wyznaczają nam ekstrema funkcji - a to jest właśnie celem optymalizacji. W analizie matematycznej pochodne liczy się algebraicznie, dlatego jest to takie uciążliwe, natomiast programy typu CAS potrafią wyliczać pochodne w sposób numeryczny, automatycznie.
W poniższych ćwiczeniach nie będziemy wchodzić w teoretyczne rozważania i wyprowadzanie wzorów dotyczących pochodnych - interesować nas będą tylko konkretne rozwiązania dla wybranych kategorii funkcji.
I ostatnia uwaga: w matematyce pochodną opisuje się następującym symbolem: 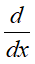i czyta „de po de iks”.

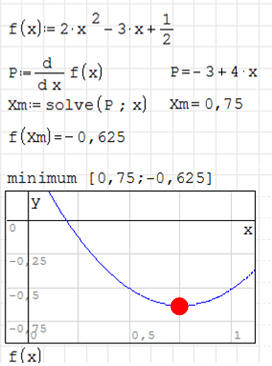
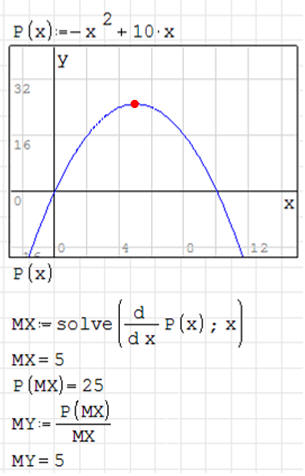
ĆWICZENIE 1 - funkcja kwadratowa

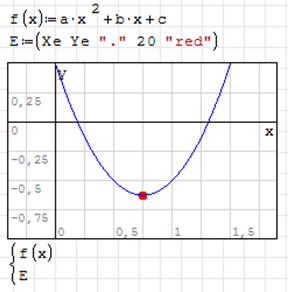
Znajdź ekstremum funkcji
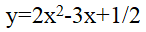
Mamy do czynienia z równaniem kwadratowym, dlatego rozwiązanie jest tylko jedno. Aby przekonać się, czy jest to maksimum, czy też minimum można sprawdzić parametr a równania kwadratowego lub też narysować wykres. Na rysunku znajdujemy kolejne przekształcenia.
• Wyliczamy pierwszą pochodną za pomocą funkcji
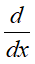
wynik znajduje się w zmiennej P,
aby zobaczyć, jak wygląda pochodna należy wcisnąć CTRL+kropka (-3+4•x)
• Szukamy pierwiastków (miejsc zerowych) równania - funkcja solve
to będzie współrzędna X naszego ekstremum - Xm
• Podstawiamy znalezioną wartość do wzoru na funkcję
to będzie współrzędna Y naszego ekstremum - Ym
Zwróć uwagę, że program potrafił wyliczyć pochodną w sposób analityczny - przekształcił równanie tak, jak uczeń na kartce papieru.
Rozwiązanie zadania. Minimum znajduje się w punkcie (0,75; -0,625).

ĆWICZENIE 2 - wielomian

Znajdź ekstrema funkcji
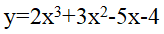
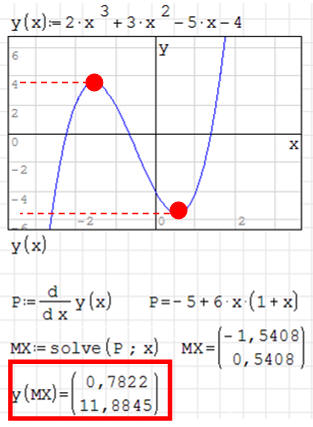
Jeśli wykonamy wykres funkcji, to okaże się, że ten wielomian ma dwa ekstrema: jedno minimum i jedno maksimum. Liczymy w standardowy sposób - rozwiązania otrzymujemy w postaci listy z dwoma elementami. Okazuje się jednak, że o ile współrzędne X są wyliczone poprawnie (tak wynika z wykresu), to już współrzędne Y naszych ekstremów są błędne - czerwona ramka. Z pobieżnej obserwacji (czerwone przerywane kreski) wynika, że powinny być mniej więcej w okolicach +4 i -5. Błąd wynika z numerycznego sposobu, w jaki program wylicza. Lepiej w takim przypadku policzyć każde rozwiązanie osobno podstawiając konkretne wyniki do funkcji. Dwa przykładowe rozwiązania pokazano poniżej!

Sposób dłuższy dodatkowe zmienne - przydatny, gdy zachodzi konieczność dalszych obliczeń.

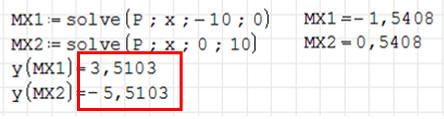
Sposób krótszy podstawiając konkretne wyniki

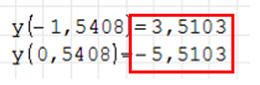
Rozwiązanie. Maksimum znajduje się w punkcie (-1,5408; 3,5104), a minimum w punkcie (0,5408; -5,5103)
Wniosek - Zawsze sprawdzaj poprawność otrzymanych wyników

ĆWICZENIE 3 - funkcja złożona

Znajdź ekstrema funkcji 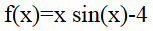w przedziale 0..15
Rysujemy najpierw wykres, aby zorientować się w przebiegu funkcji. Liczymy podobnie, jak w poprzednich przykładach. Nie liczymy automatycznie współrzędnych Y wstawiając do funkcji F listy MX - poprzednio otrzymaliśmy błędne wyniki. Lepiej jest to zrobić osobno. Tym razem jednak posłużymy się indeksami, a nie konkretnymi wartościami. Do pierwszego elementu listy MX odwołujemy się za pomocą indeksu dolnego 1 - MX1, itd. Indeks dolny wprowadzamy wciskając klawisz „[„.

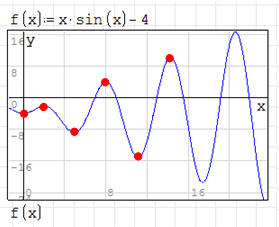
Rozwiązanie.
W przedziale (0..15) dla funkcji f(x)=x*sin(x)-4 mamy następujące ekstrema:
minima w punktach: (0; -4), (4,9132; -8,8145), (11,0855; -15,0407)
maksima w punktach: (2,0288; -2,1803), (7,9787; 3,9167), (14,2074; 10,1724)

Optymalizacja – zadania tekstowe

ĆWICZENIE 4 - powierzchnia ogródka

Gospodarz posiada 20 metrów płotu. Jakie boki powinien mieć prostokątny obszar, aby powierzchnia była jak największa?
Jest to typowe zadanie optymalizacyjne, które rozwiązuje się za pomocą pochodnej. Trudność polega na tym, że musimy mieć równanie opisujące pole powierzchni obszaru w funkcji jednego z boków, tzn. zależne tylko od jednego boku. Pole powierzchni i obwód opisują znane wzory: .
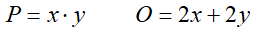Wyliczamy y z drugiego równania i wstawiamy do wzoru na P w pierwszym równaniu
UWAGA - nie musimy wstawiać, patrz kolejne ćwiczenie, 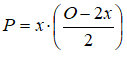, a po przekształceniach
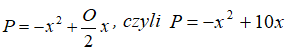
Aby zadowolić matematyków, powinno się zapisać równanie w postaci .
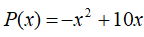Rozwiązanie. Aby powierzchnia była maksymalna (25) oba boki powinny mieć długość 5.

ĆWICZENIE 5 - konserwa

Pewien zakład produkuje puszki na konserwy. Puszki mają mieć objętość 2 litrów. Blacha kosztuje 50 groszy za 1 dm2, koszt połączeń blachy na odcinku prostym długości 1 dm wynosi 10 groszy, a na okręgu wynosi 20 groszy. Jakie powinny być wymiary konserwy, aby koszty były jak najmniejsze?
Szukamy wymiarów puszki: h i r

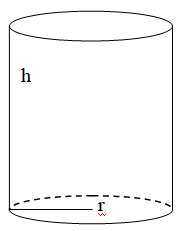
Koszt produkcji puszki, to koszt blachy i koszt połączeń: K=KB+KP
Koszt blachy, to powierzchnia blachy pomnożona przez cenę blachy: KB=PB*CB
Powierzchnia blachy składa się z prostokąta i dwóch kół.
Koszt połączeń, to długość połączenia prostego (wysokość) pomnożona przez cenę połączenia prostego i długość połączeń po okręgu (dwa obwody) pomnożona przez cenę tego połączenia: KP=DPP*CPP+DPO*CPO.
Objętość puszki wyrażamy wzorem: OP=πr2h i jest równa 2 - stąd wyliczymy promień, aby ogólne równanie miało tylko jedną zmienną h
Długość połączenia prostego: DPP=h
Długość połączeń po okręgu: DPO=2•2πr
Powierzchnia blachy: PB=2πr•h+2•πr2
UWAGA - wszystkie wzory powinny być uporządkowane i nie powinny być w postaci ułamkowej - pojawiają się błędy!!!

Odpowiedź: Aby koszt produkcji puszki był najmniejszy wysokość powinna wynosić ok. 1,8 dm, a promień ok. 0,6 dm.

Uwaga. Aby narysować wykres należy używać zmiennej o nazwie x zamiast H.

ĆWICZENIE 6 - autostrada i centrum

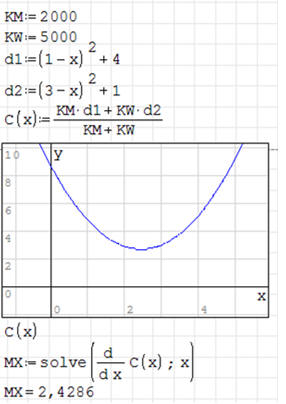
Niedaleko autostrady leżą dwie miejscowości Koty Małe (2000 mieszkańców) i Koty Wielkie (5000 mieszkańców). Położenie tych miejscowości na planie pokazuje rysunek. Można przyjąć, że obie miejscowości są punktami na mapie o współrzędnych (1, 2) i (3, -1). Władze obu miejscowości postanowiły wybudować centrum handlowe przy autostradzie tak, aby była jak najbliżej obu miejscowości uwzględniając ich liczbę mieszkańców.

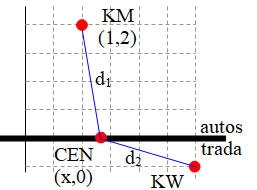
Aby centrum było w jednakowej odległości od obu miejscowości należy wyliczyć zwyczajną średnią arytmetyczną odległości. Ale chcemy uwzględnić też liczbę mieszkańców i dlatego z pomocą przychodzi nam średnia ważona. Jeżeli przyjmiemy następujące założenia: KM=2000, KW=5000, d1 - odległość KM od centrum i d2 - odległość KW od centrum, to wzór średnią ważoną będzie następujący:

.
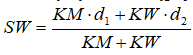
Pozostaje do wyliczenia odległość d1 i d2 - z pomocą przychodzi geometria analityczna i twierdzenie Pitagorasa.

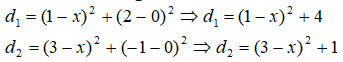
Nie musimy podstawiać do równania głównego i rozwiązywać - zrobi to za nas program.
Rozwiązanie. Centrum powinno leżeć w punkcie (2,4286; 0)

ZADANIA

Objętość walca wynosi 250. Wyznacz długość promienia walca tak, aby jego pole powierzchni całkowitej było jak najmniejsze.

Jasio wypłynął łódką na jezioro. Jego trasa miała kształt prostokąta z dwóch stron zakończonego półkolami i była długości 1 kilometra. Znajdź wymiary tej figury, której pole powierzchni będzie największe.

Na kuli o promieniu R=4 opisujemy stożek o promieniu r i wysokości h. Spośród wszystkich stożków wyznacz taki, który ma najmniejszą objętość.

Blacharz ma kawałek blachy o wymiarach 50x90 cm. Ma z niej wykonać zbiornik (otwarty z jednej strony) w kształcie prostopadłościanu. W tym celu powinien wyciąć kwadratu w rogach blachy, a następnie zagiąć i zlutować powstałą formę. Jaka powinna być długość krawędzi wyciętych kwadratów, aby objętość była jak największa? Jaka będzie to objętość i jakie będą wymiary naczynia?

Pan Nowak projektuje garaż o konstrukcji szkieletowej i długości 5 metrów, przylegający do ściany domu i zbudowany z dwóch ścian drewnianych, nakrytych płaskim, blaszanym dachem. Blacha kosztuje 30 złotych za metr kwadratowy, a sklejka do konstrukcji ścian 15 złotych za metr kwadratowy. Materiał do konstrukcji szkieletu otrzymał za darmo od znajomych. Cały garaż ma kosztować 800 złotych. Zaprojektuj wymiary garażu, które zmaksymalizują jego kubaturę.

Fabryka wykonuje kartony na soki w kształcie graniastosłupa prawidłowego czworokątnego. Jaką największą objętość może mieć ten graniastosłup, jeśli suma długości jego wszystkich krawędzi wynosi 96cm?

Trzy miejscowości A, B, C leżą przy autostradzie. Firma chce wybudować hurtownię możliwie blisko wszystkich trzech. Odległości pomiędzy miejscowościami: A-B=40, B-C=20 i A-C=60. Znajdź położenie hurtowni.

Do poprzedniego zadania dodaj informację o ilości mieszkańców każdej miejscowości: A-1000, B-500 i C-10000.

SAMODZIELNIE

1. Znajdź wartość minimalną (ekstremum) funkcji

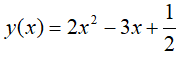
Na lekcjach matematyki szuka się współrzędnych wierzchołka funkcji kwadratowej za pomocą gotowych (podręcznikowych) wzorów

.

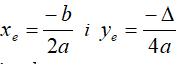Ale przecież jest wiele innych funkcji, które też mają swoje ekstrema, dla których nie mamy gotowych wzorów. Matematycy znaleźli sposób, a jest nią POCHODNA.
Co należy zrobić:
1) obliczyć pochodną z funkcji (zrobi to za nas program) – i będzie to też funkcja
2) sprawdzić, w których miejscach ta nowa funkcja ma miejsca zerowe (SOLVE)
3) wstawić te miejsca zerowe do pierwotnej funkcji – otrzymamy rzędne ekstremów

1. Wylicz współrzędne wierzchołka za pomocą matematycznych wzorów
2. Wylicz pochodną funkcji y(x) stosując plecenie
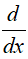
Wynik zapisz w zmiennej, np. p(x) lub po prostu p
3. Wyświetl równanie pochodnej – zastosuj polecenie CTRL+KROPKA
4. Odciętą wylicz stosując polecenie SOLVE dla pochodnej.
5. Rzędną wylicz wstawiając zmienną odciętą do funkcji.
6. Narysuj wykres funkcji
7. Umieść na wykresie punkt ekstremalny tej paraboli
UWAGA – rozwiązanie pokazano trzema sposobami – wykonaj wszystkimi trzema;
punkt ekstremalny (wierzchołek paraboli) powinien pokrywać się z wyliczonym w p. 3 i 4

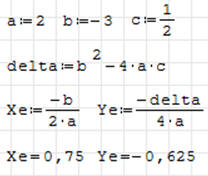
2. Znajdź ekstrema funkcji 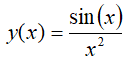w przedziale (0, 20)
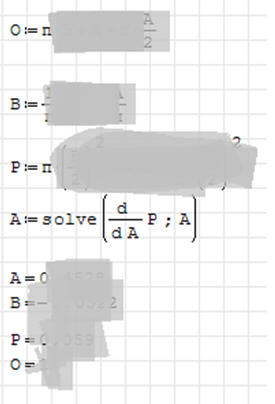
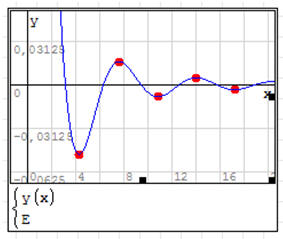
1. Narysuj wykres funkcji y(x)
2. Wylicz pochodną funkcji y(x)
3. Wylicz odcięte (współrzędne x) ekstremów pochodnej w przedziale (0, 20)
4. Wylicz rzędne (współrzędne y) ekstremów pochodnej
stosując operacje pokazane na obrazku
5. Nanieś wyznaczone ekstrema na wykres funkcji – czerwone punkty
UWAGA – jeżeli na jednym arkuszu rozwiązujesz kilka zadań – pamiętaj, że zmienne o takich samych nazwach mogą sobie „przeszkadzać”

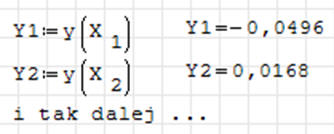
3. Jasio wypłynął łódką na jezioro. Jego trasa miała kształt prostokąta z trzech stron zakończonego półkolami i była długości 1 kilometra. Znajdź wymiary tej figury, tak aby jej pole powierzchni będzie największe.
Przykładowy rysunek trasy Jasia, gdzie a i b oznaczają boki prostokąta. Obwód – trasa łódki, to długa prosta i dwie połowy obwodu małych kół i jedna połowa dużego koła. Pole powierzchni składa się z prostokąta, dwóch połówek małych kół i jednej połówki dużego koła:

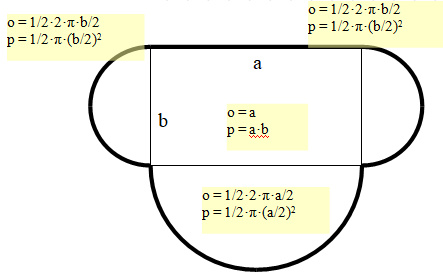
1. Zapisz wzór na obwód
2. Pamiętając, że obwód jest równy 1, wylicz z wzoru na obwód bok b – wynik w zmiennej b
3. Zapisz wzór na pole – wynik w zmiennej P
4. Wylicz ekstremalną wartość boku a szukając pierwiastków pochodnej funkcji P
Ile to jest w metrach?
5. Wylicz ekstremalną wartość zmiennej b.
Ile to jest w metrach?
Co możesz powiedzieć o tym boku.
6. Narysuj schematycznie powierzchnię jeziora
Wstaw-Obrazek-Utwórz – i można rysować
7. Wylicz pole powierzchni jeziora, jakie opłynął Jasio
Ile to jest w metrach kwadratowych?
UWAGA – jeżeli na jednym arkuszu rozwiązujesz kilka zadań – pamiętaj, że zmienne o takich samych nazwach mogą sobie „przeszkadzać”