mgr inż. Wacław Libront * Bobowa 2017-2019

ZSO Bobowa, ul. Długoszowskich 1, 38-350 Bobowa, tel: 0183514009, fax: 0183530221, email: sekretariat@zsobobowa.eu, www: zsobobowa.eu
mgr inż. Wacław Libront * Bobowa 2017-2019

ZSO Bobowa, ul. Długoszowskich 1, 38-350 Bobowa, tel: 0183514009, fax: 0183530221, email: sekretariat@zsobobowa.eu, www: zsobobowa.eu
Z matematycznego punktu widzenia całkowanie jest bardzo skomplikowanym procesem, najeżonym mnóstwem założeń, twierdzeń, wzorów i symboli. Z czysto użytkowego (i inżynierskiego) punktu widzenia całkowanie polega na wyliczeniu długości, pola powierzchni lub objętości przedmiotu. Oczywiście, aby było to możliwe, wielkości te należy opisać matematycznym równaniem. Użycie komputerów sprawia, że niepotrzebne są także analityczne metody, czyli skomplikowane wyprowadzanie wzorów. Te dziwne wzory, np. na objętość kuli czy walca biorą się właśnie z analitycznego całkowania.
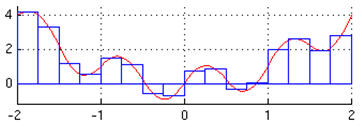
W jaki sposób całkuje komputer? Czerwony wykres pokazuje przebieg jakiejś
funkcji, a my chcemy policzyć pole powierzchni pod tym wykresem. W tym celu
dzielimy cały obszar na niewielkie prostokąty, wyliczamy ich pola powierzchni i
sumujemy. Oczywiście będzie to wynik niedokładny, ale zawsze można zmniejszyć
bok prostokąta (tym samy zwiększyć ilość i dokładność) lub zamiast prostokątów
zastosować trapezy albo jeden z boków zastąpić krzywą.
W matematyce całkowanie oznaczamy symbolem
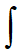 a równanie
a równanie
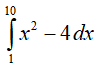 oznacza, że liczymy pole powierzchni
pod wykresem ograniczonym krzywą o równaniu x2-4 w przedziale od 1 do
10. Symbol dx (czytamy „de iks”) dotyczy zmiennej z naszego równania.
oznacza, że liczymy pole powierzchni
pod wykresem ograniczonym krzywą o równaniu x2-4 w przedziale od 1 do
10. Symbol dx (czytamy „de iks”) dotyczy zmiennej z naszego równania.
ĆWICZENIE 1 - pole trójkąta
Oblicz pole powierzchni pod wykresem funkcji y=2x w przedziale od 0 do 2.
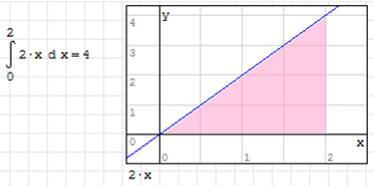
Wyliczenie nie przedstawia żadnej trudności. Dla zobrazowania narysujmy jeszcze wykres funkcji. Okazuje się, że pole powierzchni pod wykresem, to pole trójkąta o boku 2 i wysokości 4, czyli rzeczywiście jest równe 4.
ĆWICZENIE 2 - pole koła
Oblicz pole powierzchni ograniczonej krzywą
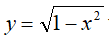 w przedziale od -1 do +1.
w przedziale od -1 do +1.
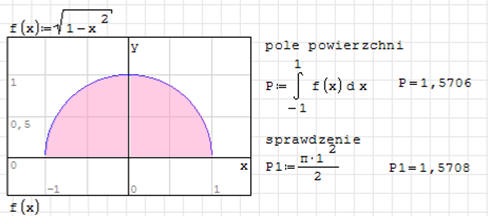
Po narysowaniu wykresu okazuje się, że mamy do czynienia z kołem (dokładnie z półkolem), którego wzór na pole doskonale jest znamy. Dla sprawdzenia poprawności całkowania zastosujemy zwykły wzór.
ĆWICZENIE 3 - sinus
Wylicz pole powierzchni pod krzywą y=sin(x) w przedziale 0 do 180 stopni.
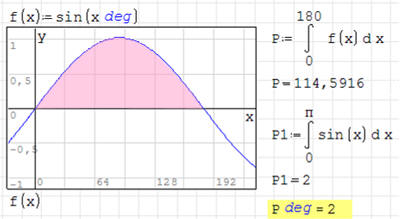
Obliczenia nie przedstawiają żadnych trudności. Należy
uwzględnić jednak zamianę radianów na stopnie podczas obliczania całki. Dla
sprawdzenia policzono również całkę bez zamiany na radiany (pole P1=2).
Sprawdzenie wyników daje takie same rezultaty.
ĆWICZENIE 4 - jezioro
W parku ma powstać jezioro o kształcie wyznaczonym przez krzywą określoną równaniem y=-x2+5x-2 i oś X. Wylicz pole powierzchni tego jeziora.
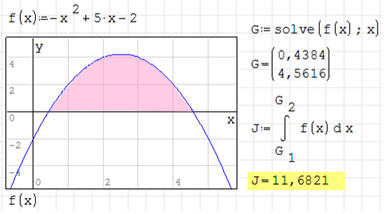
Wykres pokazuje kształt jeziora. Jedynym problemem są punkty graniczne jeziora. W naszym przypadku będą to pierwiastki równania kwadratowego, które wyznaczymy za pomocą funkcji solve.
ĆWICZENIE 5 - łezka
W parku ma powstać jezioro o kształcie wyznaczonym przez dwie
krzywe określone równaniami: 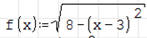 ,
,
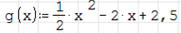 i osią X. Wylicz pole powierzchni
tego jeziora
i osią X. Wylicz pole powierzchni
tego jeziora
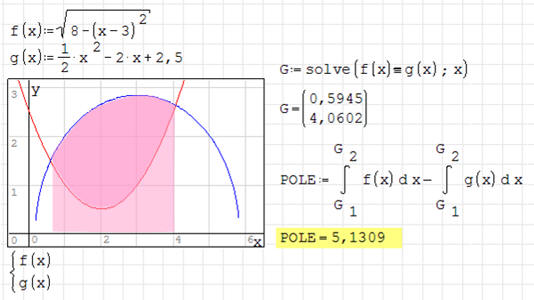
Rysunek pokazuje powierzchnię jeziora. Podobnie, jak w
poprzednim zadaniu należy znaleźć punkty graniczne (przecięcie się dwóch
krzywych), które jednocześnie stają się granicami całkowania. Różnica pól pod
krzywymi daje poszukiwane pole (obszar ciemniejszy).
Długości również obliczamy metodami całkowania. Jeśli liczymy
numerycznie (np. na arkuszu kalkulacyjnym), to sumujemy przekątne prostokątów (tw.
Pitagorasa). Nieco bardziej skomplikowanie wygląda całkowanie algebraiczne (w
programie typu CAS) i wzór na długość krzywej określony jest następującym
równaniem: 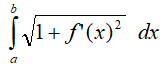 . Co ono oznacza?
. Co ono oznacza?
• f(x) - funkcja, która określa kształt krzywej
• f’(x) - liczymy pochodną funkcji
• f’(x)2 - podnosimy pochodną do kwadratu
• 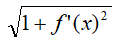 - dodajemy jeden i pierwiastkujemy
- dodajemy jeden i pierwiastkujemy
• 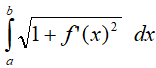 - teraz możemy całkować w przedziale
(a,b)
- teraz możemy całkować w przedziale
(a,b)
• Wynikiem całkowania jest długość krzywej
ĆWICZENIE 6 - przekątna
Oblicz długość krzywej, którą opisuje równanie y=2x w przedziale od 0 do 2.
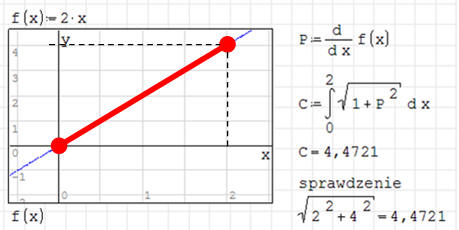
Na rysunku pokazano krzywą, której długość wyliczamy
(czerwony odcinek). Najpierw liczymy pochodną P, a po wstawieniu do wzoru
otrzymujemy długość. Sprawdzenie z pomocą tw. Pitagorasa.
ĆWICZENIE 7 - długość łuku
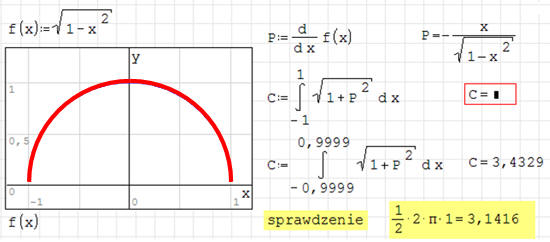
Oblicz długość krzywej, którą opisuje krzywa
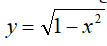 w przedziale od -1 do +1.
w przedziale od -1 do +1.
Jeżeli będziemy rozwiązywać to zadanie w sposób standardowy okaże się, że nie zdołamy policzyć długości w przedziale (-1, 1). Z matematycznego punktu widzenia okazuje się, że dla podanych wartości brzegowych nie istnieje rozwiązanie. Możemy jednak przyjąć wartości bardzo bliskie, np. (-0,9999, 0,9999) - otrzymamy wynik przybliżony.
ĆWICZENIE 8 - sinusoida
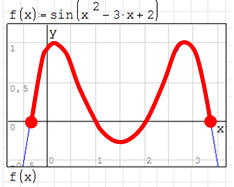
Wylicz długość sinusoidy określonej równaniem y=sin(x2-3x+2), w przedziale, który wyznaczają punkty przecięcia krzywej z osią X (patrz obrazek).
Za pomocą funkcji solve znajdujemy właściwe punkty i podstawiamy, jako granice całkowania.
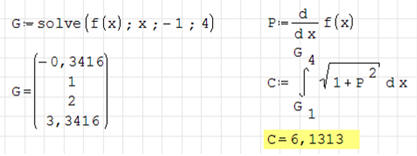
ĆWICZENIE 9 - praca rakiety
Oblicz pracę, jaką należy wykonać, aby podnieść z powierzchni
Ziemi ciało o masie 3000000 kg (rakieta Saturn) na wysokość 10 metrów.
Pracę w fizyce liczymy z następującego wzoru:
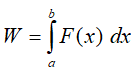
Na wysokości x nad powierzchnią ziemi siła przyciągania wynosi:
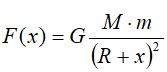 ,
,
gdzie G - stała grawitacji, M - masa Ziemi, m - masa rakiety, R - promień Ziemi.
Ponieważ w programie SMathStudio mamy problemy z całkowaniem w jednostkach, dlatego wartości wszystkich stałych zamieniamy na układ SI. Wtedy pracę otrzymujemy w dżulach [J] – i możemy całkować bez używania jednostek.
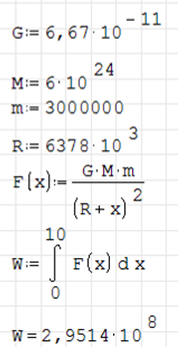
ĆWICZENIE 10 - droga pojazdu
Samochód poruszał się z zmienną prędkością, którą opisuje
następujący wzór: 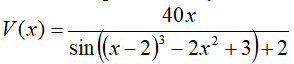 ,
,
gdzie x oznacza czas. Jaką drogę przejechał ten samochód w
czasie 4 pierwszych godzin?
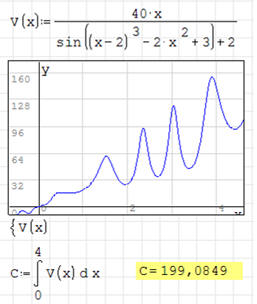
Drogę w fizyce liczymy z ogólnego wzoru: , gdzie x oznacza czas ruchu pojazdu.
ZADANIA
Zadanie 1
Masz dane dwie funkcje kwadratowe
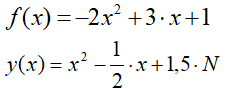
Znajdź miejsca zerowe, punkty wspólne i ekstremalne dla obu funkcji
Wylicz pola powierzchni pod wykresami i pole powierzchni części wspólnej
Wylicz długości krzywych pomiędzy miejscami zerowymi i punktami wspólnymi
Narysuj wykres i umieść na nim obie krzywe oraz charakterystyczne punkty
Zadanie 2
Sprawdź za pomocą całkowania numerycznego prawdziwość podstawowych wzorów
geometrii na płaszczyźnie (pole i długość brzegu dla: kwadratu, trójkąta, koła,
trapezu.
UWAGA - wyznacz równania prostych (krzywych), które ograniczają te figury.
Całkowanie – co to takiego? W najprostszym ujęciu chodzi o policzenie pola powierzchni, objętości lub długości. Ze szkoły znamy wiele gotowych wzorów. Jednak, gdy figura jest skomplikowana i takiego gotowego wzoru nie znamy z pomocą przychodzi całkowanie. Na lekcjach matematyki wyższej będziesz uczył się, jak całkować algebraicznie (rozwiązywanie równań), ale programy typu CAS potrafią to robić od razu metodami numerycznymi.
ZADANIE - TUNEL
Wlot do tunelu pokazuje poniższy rysunek.
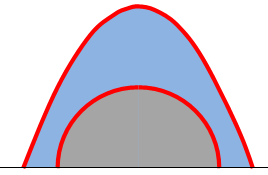
Obie ograniczające brzegi tunelu czerwone krzywe (okrąg i parabola) opisują
następujące równania: 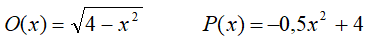 .
.
Wylicz pole powierzchni wlotu do tunelu (niebieski kolor), które niezbędne
będzie do wyliczenia kosztów malowania. Wylicz również długość linii brzegowej
(czerwony kolor) – koszt metalowych wzmocnień.
Aby wyliczyć pole powierzchni oznaczonej niebieskim kolorem, należy całe pole
pod parabolą P(x) pomniejszyć o pole połowy okręgu O(x). Pola powierzchni
wyliczymy, gdy będziemy mieli współrzędne punktów przecięcia się obu krzywych z
osią OX – powierzchnią ziemi.
WYKRES
1. Narysuj na wspólnym wykresie obie krzywe
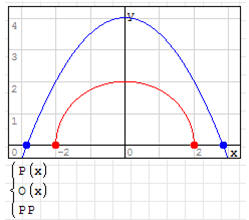
2. Za pomocą polecenia SOLVE wylicz miejsca zerowe obu krzywych
Zapisz je w zmiennych PX i OX (każda zawiera dwie wartości)
3. Zaznacz kolorowymi punktami miejsca zerowe
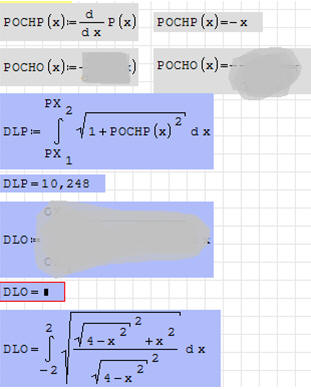
POLE POWIERZCHNI
1. Wylicz pole powierzchni pod parabolą (PPP) i okręgiem (PPO)
2. Wylicz pole powierzchni przeznaczonej do malowania – różnica PPP i PPO

DŁUGOŚĆ KRZYWEJ
1. Wylicz pochodne obu funkcji i zapisz je w postaci funkcji POCHP(x) i POCHO(x)
2. Wylicz długości stosując następujący wzór:
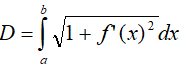
gdzie f’(x) jest pochodną funkcji f(x)
UWAGA - obliczenie długości okręgu nie daje poprawnego wyniku, gdyż funkcja O(x) nie ma rozwiązań w wyznaczonych punktach ( 2,0) i (2,0). Aby otrzymać wynik (przybliżony) zmieniamy parametry brzegowe zwiększając dolny przedział i zmniejszając górny przedział o bardzo małą wielkość, np. o 0,00001
3. Wylicz długość całkowitą sumując długości obu krzywych

ZADANIE - RAKIETA
Oblicz pracę, jaką należy wykonać, aby podnieść z powierzchni Ziemi ciało o
masie 3000000 kg (rakieta Saturn) na wysokość 1000 metrów.
Pracę w fizyce liczymy z następującego wzoru:
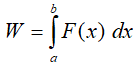 .
.
Na wysokości h nad powierzchnią ziemi siła przyciągania wynosi:
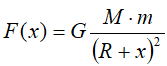 ,
,
gdzie G - stała grawitacji G=6.67•10-11, M - masa Ziemi M=6•1024, m - masa rakiety, R - promień Ziemi R=6378•103.Wszystkie wartości podano w jednostkach układu SI (metr, kilogram, sekunda)
1. Wylicz pracę całkowitą, którą wykona rakieta (paliwo rakiety) po przelocie
na odległość 1000m
2. Narysuj wykres pokazujący wielkość działającej siły w funkcji odległości od
powierzchni ziemi