Lekcja 8 

Obliczenia statystyczne

1. Wstęp
2. Podstawowe pojęcia
3. Rozkład normalny Gaussa
4. Test Studenta
5. SAMODZIELNIE
6. lekcja 8 - statystyka.sm

Wstęp

Statystyka jest nauką, która zajmuje się zbieraniem danych i ich analizą. Praca statystyka polega głównie na zebraniu dużej ilości danych opisujących jakieś zjawisko, ich analizie i interpretacji. Nie będziemy zajmować się oczywiście zbieraniem danych, lecz tylko ich analizą, czyli matematycznym wyliczeniem różnych zależności zachodzących pomiędzy liczbami, a także postaramy się wyciągać wnioski z tak otrzymanych wyników.
Wiele badanych zjawisk z życia człowieka charakteryzuje się losowością (np. wzrost ludzi, wynik wyborów, itp.) i nie jest możliwe przebadanie wszystkich z danej populacji, aby stwierdzić naprawdę „jak jest”. Możemy za to przebadać grupę wybranych osób, wyliczyć zależności, i na tej podstawie wyciągnąć wnioski, co do całości. Statystyka jest dzisiaj szeroko stosowana, m.in. w badaniach demografii, psychologii, socjologii, termodynamice, fizyce kwantowej, astronomii, ekonomii, demografii, itd.

Podstawowe pojęcia statystyki

Średnia arytmetyczna
Najbardziej intuicyjna miara oceny danej serii pomiarów. Sumujemy pomiary i dzielimy przez ich ilość.

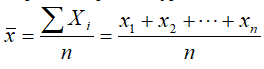
Średnia harmoniczna
Za pomocą średniej harmonicznej obliczamy np. średnią prędkość jazdy samochodem.

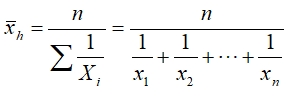
Średnia geometryczna
W statystyce opisuje się średnie tempo zmian jakiegoś zjawiska lub miarę przeciętnego poziomu wartości cech badanych elementów. Stosuje się ją, gdy mamy do czynienia z rozkładami logarytmicznymi.

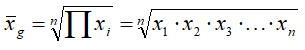
Średnia kwadratowa
W statystyce opisuje rząd wielkości serii danych, przydatnych, gdy liczby różnią się znakiem. Średnia kwadratowa różnic wartości zmiennej i średniej arytmetycznej jest nazywana odchyleniem standardowym i pełni bardzo ważną funkcję w statystyce.

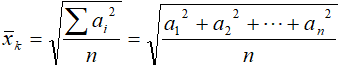
Średnia ważona
Jeżeli badamy elementy, z których każdy posiada przypisaną jakąś wagę, wpływającą mniej lub bardziej na zjawisko, to średnia ważona najlepiej oddaje całościowy charakter próby. Na przykład każdej ocenie nauczyciel przypisuje wagę w zależności od ważności. Na przykład sprawdzian pisemny bardziej znacząca ocena - waga 3, odpowiedź ustna mniej znacząca - waga 2, zadanie domowe najmniej znaczące - waga 1, itp. Średnia arytmetyczna nie uwzględnia tych dodatkowych cech. Jeżeli wszystkie oceny mają identyczną wagę, wtedy średnia ważona jest równa średniej arytmetycznej.

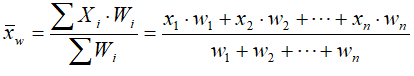
, gdzie X - badany element, W - waga badanego elementu.

Dominanta
Wartość, która występuje najczęściej w badanym zbiorze – największą ilość razy.

Mediana
Mediana jest wartością znajdującą się na środku zbioru. Gdy badany zbiór ma parzystą liczbę elementów, obliczamy średnią z dwóch leżących wokół środka.

Wariancja
Wariancja tak naprawdę nic nie wyjaśnia, lecz jest potrzebna przy wielu statystycznych obliczeniach, m.in. przy odchyleniu standardowym.

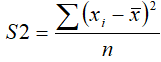
Najpierw musimy mieć średnią arytmetyczną, którą odejmujemy od każdego elementu zbioru. Różnicę podnosimy do kwadratu i wszystkie sumujemy. Na końcu sumę różnic dzielimy przez liczbę elementów.

Odchylenie standardowe
Jeśli mamy obliczoną średnią arytmetyczną, to odchylenie standardowe pokazuje nam, jak bardzo „rozrzucone” są poszczególne wyniki od tej średniej. Można też powiedzieć, jak daleko znajdują się od średniej. Na przykład średnia ocen wystawionych przez nauczyciela wynosi 3,5, a odchylenie – 2. Oznacza to, że oceny mieszczą się w przedziale 1,5 – 5,5.

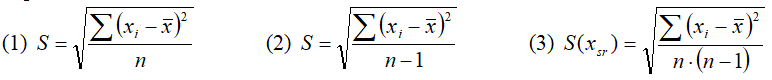
Jeżeli przebadaliśmy całą badaną grupę stosujemy wzór (1), tzw. odchylenie standardowe – bardzo rzadko mamy do czynienia z taką sytuacją. Jeżeli przebadaliśmy tylko część grupy stosujemy wzór (2) – odchylenie standardowe pojedynczego pomiaru. Natomiast wzór (3), tzw. niepewność standardowa pokazuje błąd odchylenia standardowego.

Współczynnik zmienności
Współczynnik zmienności pokazuje nam, jak silne jest zróżnicowanie danych. Odchylenie standardowe dzielimy przez średnią arytmetyczną, a wynik prezentujemy w procentach. Jeżeli współczynnik mamy w granicach 0-20% to mówimy, że zróżnicowanie jest małe. Jeżeli powyżej 60% - zróżnicowanie bardzo duże.

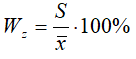
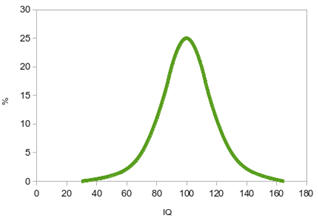
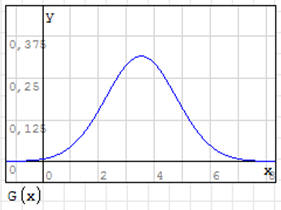
Rozkład normalny Gaussa
Jest to wykres (tzw. krzywa dzwonowa), który odgrywa bardzo ważną rolę w statystycznym opisie zagadnień przyrodniczych, przemysłowych, medycznych, społecznych, itp. Poziom inteligencji, wzrost, oceny wystawiane przez nauczyciela, itp. wszystko to oscyluje wokół jakiejś średniej. Krzywa Gaussa pokazuje, jak bardzo poszczególne pomiary odchylone są od tej średniej. Wszystkie prawidłowe procesy będą oscylowały oczywiście wokół średniej, a każde zjawisko niepożądane będzie dawało pomiary znacznie odbiegające od tej średniej. Innymi słowy: jeżeli przeprowadzone przez nas badanie będzie przypominało rozkład Gaussa, możemy powiedzieć, że jest to zjawisko normalne, bez żadnych anomalii. Przykładowa krzywa na rysunku pokazuje np. rozkład poziomu inteligencji w badanej grupie.
Funkcja opisująca rozkład normalny ma postać:

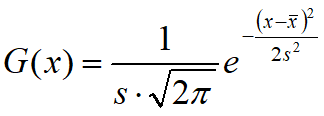
gdzie s - odchylenie standardowe, ¬x - średnia arytmetyczna

Korelacja - powiązanie, zależność
Korelacja mówi nam, jak bardzo powiązane są ze sobą dwa zestawy pomiarów (dwie tabele z danymi). Na przykład, jaki związek ma frekwencja na zajęciach z wynikami osiąganymi na egzaminie.
Wielkość tę określa się też czasami, jako współczynnik korelacji liniowej Pearson’a lub χ2 (chi kwadrat). Jeżeli wartość korelacji przybiera wartości bliskie zeru, mówimy o całkowitym braku korelacji (frekwencja nie ma wpływu na egzaminy). Jeżeli korelacja przyjmuje wartości bliskie 1 (100%), mówimy o dużej zależności.

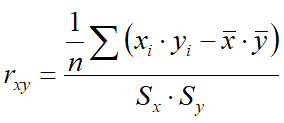
ĆWICZENIE 1 - średnia arytmetyczna, geometryczna i harmoniczna

Nauczyciel wystawił następujące oceny: (2, 5, 5, 4, 3, 3, 5, 2, 2, 4). Wylicz średnią arytmetyczną, geometryczną i harmoniczną.

• Wektory tworzymy trzeba sposobami: wpisując polecenie MAT, wybierając z menu: Wstaw / Macierz lub wciskając CTRL+M (wektor może być pionowy O lub poziomy C)
• Obliczamy długość wektora nA i nC - ilość elementów za pomocą polecenia LENGTH
• Sumowanie elementów ∑O wektora wykonujemy za pomocą polecenia SUM(1) lub SUM(4)
• Obliczając średnią arytmetyczną ŚRa można posłużyć się wersją mniej skomplikowaną (nie używamy indeksów) lecz może ona dawać niepoprawne wyniki w bardziej złożonych obliczeniach
• Średnia harmoniczna ŚRh musi być liczona za pomocą polecenia SUM(4) – nie działa sumowanie z wersją uproszczoną
• Średnia geometryczna ŚRg - pierwiastek n-tego stopnia - CTRL+\, mnożenie - polecenie PRODUCT

ĆWICZENIE 2 - średnia ważona

Nauczyciel wystawił następujące oceny: (2, 5, 5, 4, 3, 3, 5, 2, 2, 4), każda ocena posiada określoną wagę: (1, 3, 3, 3, 2, 2, 2, 2, 1, 1). Wylicz średnią ważoną.
Sumujemy iloczyn oceny i jej wagi, a następnie dzielimy przez sumę wag. Również wersja uproszczona sumowania nie działa.

ĆWICZENIE 3 - odchylnie standardowe

Dla ocen z poprzednich ćwiczeń oblicz odchylenie standardowe.
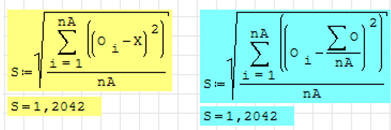
Jeżeli mamy policzone średnią X i wariancję S2, rachunki wyglądają zdecydowanie prościej. Odchylenie policzono w zmiennej S.

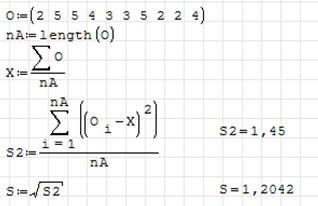
To samo odchylenie możemy policzyć jednym wzorem, korzystając z wcześniej obliczonej średniej (żółte) lub bez wcześniejszego obliczenia średniej (niebieskie)

ĆWICZENIE 4 - współczynnik zmienności

Dla ocen z poprzednich ćwiczeń oblicz współczynnik zmienności.
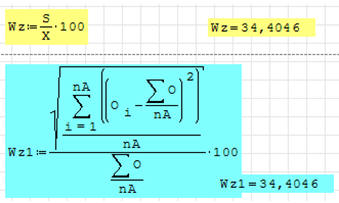
Jeżeli mamy policzone średnią X i odchylenie standardowe S rachunki wyglądają zdecydowanie prościej – współczynnik policzony w zmiennej Wz. Jeżeli nie policzono wcześniej średniej i odchylenia, jeden wzór pokazany w niebieskim polu.

ĆWICZENIE 5 - dobry uczeń

Dla następujących ocen:
(4, 5, 5, 5, 5, 5, 5, 5, 6, 5),
oblicz odchylenie standardowe i współczynnik zmienności.
Zdecydowanie mniejsze zróżnicowanie ocen, dlatego oba parametry mniejsze.
 

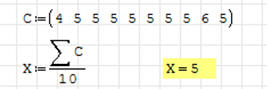
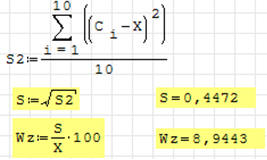
ĆWICZENIE 6 - krzywa Gaussa

Wykreśl krzywe Gaussa dla obu zestawów ocen

Pierwsza krzywa wykreślona za pomocą oryginalnego wzoru, w drugiej zastosowano funkcję EXP - równanie wygląda zdecydowanie „lepiej”.

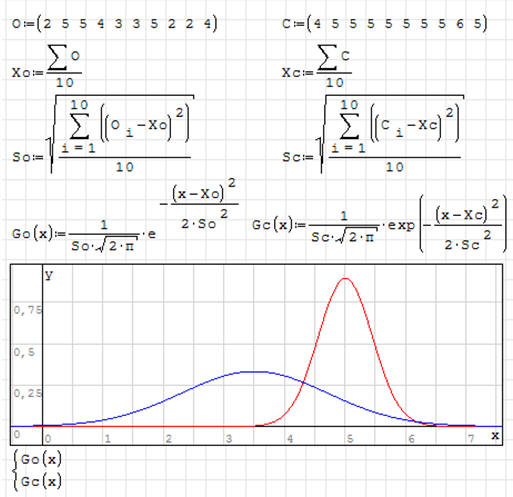
Krzywe pokazują rozkłady poszczególnych ocen. Pierwsza krzywa - uczeń „normalny”. Druga krzywa - uczeń „bardzo dobry”.

Jeżeli zestawy ocen dotyczyłyby nauczycieli, moglibyśmy powiedzieć, że nauczyciel pierwszy jest zupełnie „standardowy”, a nauczyciel drugi jest zdecydowanie zbyt „łagodny”.

ĆWICZENIE 7 - korelacja

Mamy dane oceny dla dwóch uczniów z tej samej klasy (zielone) i z różnych klas (żółte). Porównaj korelacje i wyciągnij wnioski.

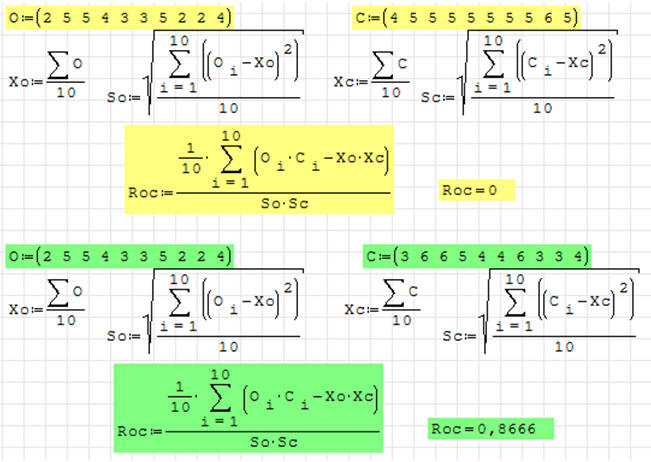
Interpretacja:
Żółte oceny - korelacja równa 0, czyli całkowity brak powiązań pomiędzy ocenami. Uczniowie (przeciętny i dobry) pisali różne sprawdziany - np. oceny uczniów z dwóch różnych klas.
Zielone oceny - korelacja bliska 0,9 (90%) - bardzo wysoka zgodność ocen. Uczniowie (przeciętny i dobry) pisali identyczne sprawdziany, u tego samego nauczyciela.

ĆWICZENIE 8 - arkusz ocen

Pokazana na rysunku tablica (5x7) zawiera arkusz ocen końcowych w pewnej klasie. Wylicz średnią całej klasy, średnią dla pierwszego przedmiotu i drugiego ucznia.
• Liczba wierszy - funkcja ROWS
• Liczba kolumn - funkcja COLS
• Średnia wszystkich ocen w tabeli
w wersji uproszczonej podajemy nazwę tabeli bez indeksów, liczba elementów jest iloczynem wierszy i kolumn. Wersja rozbudowana składa się z podwójnego sumowania (sumowanie po kolumnach wewnątrz sumowania po wierszach)
• Średnia z pierwszej kolumny - przedmiot
aby podsumować elementy pierwszej kolumny należy ustawić indeksowanie po wszystkich wierszach i podzielić przez ilość wierszy
• Średnia z drugiego wiersza - uczeń
aby podsumować elementy drugiego wiersza należy ustawić indeksowanie po wszystkich kolumnach i podzielić przez ilość kolumn

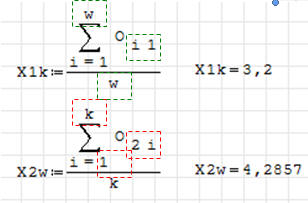
Jeszcze więcej o porównywaniu wyników badań

Test t Studenta
Gdy porównujemy ze sobą dwie grupy, to różnice występują zawsze, to jeszcze jednak o niczym nie świadczy. Dopiero, gdy test wykaże, że te różnice są odpowiednio duże - mówimy, że są statystycznie istotne. Co to znaczy odpowiednio duże (statystycznie istotne)? Otóż przyjmujemy na wstępie (hipoteza), że najwyżej 5% z badanej grupy (poziom istotności 0,05) może się różnić. Jeśli tak rzeczywiście będzie, to znaczy, że badane grupy się statystycznie nie różnią, a zaobserwowane wyniki nie są statystycznie istotne. W typowych badaniach przyjmuje się z reguły poziom istotności 0,05 lub 0,01.
Test t Studenta jest najczęściej stosowaną metodą oceny różnic w badanych grupach. Czy podawany pacjentom lek leczy? Czy kolejna dieta-cud ma sen? Czy wyniki z egzaminu mieszczą się w średniej krajowej? Innymi słowy, jak bardzo są ze sobą skorelowane przeprowadzone badania w dwóch próbach?
Mamy trzy rodzaje testów w zależności od rodzajów grup.

Test dla prób niezależnych (dwie różne grupy ludzi). Chcemy na przykład określić wpływ leku na wyleczalność jakiejś choroby podając lek jednej grupie, a drugiej podając placebo.

Test dla prób zależnych (jedna grupa ludzi) zachodzi wówczas, gdy mamy tą samą grupę ludzi i poddajemy ich obserwacji przed i po. Możemy np., zmierzyć samopoczucie badanej grupy przed i po podaniu leków.

Test dla pojedynczej próby (jedna grupa ludzi) - posługujemy się nim wtedy, gdy chcemy zbadać zależność pomiędzy średnią z danego badania a średnią uzyskaną np. z literatury. Porównujemy np. średnią z egzaminu w naszej szkole ze średnią egzaminu w całej Polsce.

Wzory
Patrząc na poniższe wzory odnieść można wrażenie, że „to jest straszne”, ale literatura podaje, że testy te są jednymi z mniej skomplikowanych!
• grupy niezależne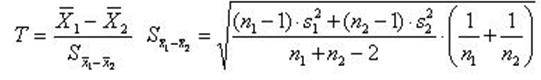
• grupy zależne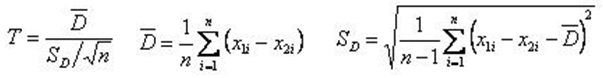
• pojedyncza próba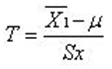

Dygresja. Dlaczego test Studenta? Otóż na początku XX wieku pewien browar zatrudniał studentów do testowania swoich produktów, a jeden ze studentów wymyślił te „straszne” wzory, które w końcowym efekcie dały firmie ogromne zyski.

Potrafimy już policzyć. Ale, o czym nam mówi otrzymany wynik? I jak w praktyce wygląda analiza? Po pierwsze hipoteza. Zakładamy, że otrzymane rezultaty są istotne (bądź nieistotne) statystycznie. Co to znaczy istotne? To oznacza, że badany lek jednak leczy, że dieta ma wpływ na chudnięcie, itd. Po drugie poziom istotności, czyli jak bardzo chcemy ufać naszym wynikom. W praktyce przyjmuje się dwa poziomy: 0,01 lub 0,05. Załóżmy, że przeprowadziliśmy 100 prób (100 badań). Jeżeli przy założonym poziomie 0,05 ponad 5 badań (5%) różni się od siebie, to próby są statystycznie niezależne od siebie, różnica jest statystycznie istotna, albo inaczej hipoteza się nie sprawdziła. Lek jednak nie leczy tak, jakbyśmy się tego spodziewali, bo ponad 5% badanych nie wyzdrowiało.

SAMODZIELNIE

Statystyka zajmuje się gromadzeniem i analizą danych. A w praktyce? Na podstawie badania jakiejś losowo wybranej grupy (np. uczniów) próbujemy scharakteryzować całą szkołę. Oczywiście najlepiej byłoby przebadać całą szkołę, ale… Na podstawie takich badań można powiedzieć czy dana szkoła jest „normalna”, tzn. czy nie odbiega zanadto od innych szkół.

ZADANIE – OCENY
ŚREDNIE
Pewien uczeń otrzymał z pewnego przedmiotu następujące oceny: 2, 5, 5, 4, 3, 3, 5, 2, 2, 4. Pewien nauczyciel stosuje następujące kryterium wystawiania oceny końcowej: ocena końcowa jest najlepszą spośród trzech średnich: arytmetycznej, harmonicznej i geometrycznej dla tych ocen. Wylicz te średnie.

1. Zapisz oceny w postaci wektora (macierzy jednowymiarowej, listy) o nazwie OCENY
2. Wylicz ilość ocen stosując polecenie LENGTH – zapisz ilość w zmiennej N
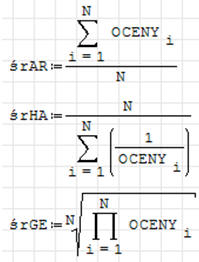
3. Wylicz średnią arytmetyczną z wzoru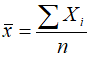
Funkcję sumowania uzyskamy po wpisaniu polecenia SUM i wybraniu polecenia SUM(4)
4. Wylicz średnią harmoniczną z wzoru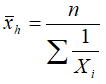
5. Wylicz średnią geometryczną z wzoru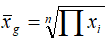
Funkcję mnożenia uzyskamy po wpisaniu polecenia PRODUCT

ODCHYLENIE
Odchylenie standardowe sprawdza, jak bardzo rozrzucone są oceny – jak bardzo odstają od średniej arytmetycznej ucznia. Współczynnik zmienności pokazuje podobną ocenę w procentach.
6. Wylicz odchylenie standardowe z wzoru:
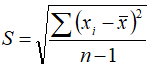
7. Wylicz współczynnik zmienności z wzoru:
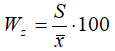
Jeżeli współczynnik zmienności jest mały, znaczy to, że uczeń prezentuje jednakowy poziom – ma podobne oceny. Jeżeli oceny są bardzo zróżnicowane – współczynnik jest wysoki.

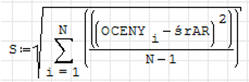
KRZYWA GAUSSA
Wszystkie statystyczne zależności obrazuje bardzo dokładnie krzywa Gaussa. Pokazuje ona prawdopodobieństwo wystąpienia jakiejś oceny.

8. Pokaż na wykresie Gausa rozkład ocen opisywanego ucznia.

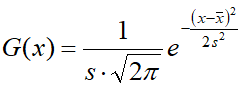
Ponieważ wszystkie zmienne występujące w funkcji G(x) mamy już wyliczone (średnia – i odchylenie – S), dlatego wystarczy poprawnie napisać funkcję.
symbol „e” oznacza liczbę Nepera (lub Eulera) i jest to podstawa logarytmu naturalnego – można ją wybrać z menu lub posłużyć się funkcję EXP

KORELACJA
Korelacja opisuje powiązania pomiędzy badanymi seriami danych. Jeśli korelacja jest wysoka (bliska 100%) oznacza to, że te serie danych dotyczą np. uczniów tej samej klasy, próbek tej samej partii materiału, itp.
Wzór opisujący korelację ma postać: .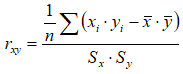

Widać z niego, że należy policzyć średnią arytmetyczną i odchylenie standardowe dla ocen drugiego ucznia.

Inny uczeń tej szkoły ma następujące oceny z pewnego przedmiotu: 4, 5, 5, 5, 5, 5, 5, 5, 6, 5.
9. Sprawdź, jaka jest korelacja pomiędzy ocenami obu uczniów.

Po obliczeniu - dla badanych zestawów ocen korelacja wynosi 0 – oceny uczniów są zupełnie rozbieżne – dwaj różni uczniowie