Lekcja 8

Rekurencja w C++

1. rekurencja
2. silnia
3. euklides
4. fibonacci
5. wspak
6. horner
7. zadania
8. rozwiązania

Rekurencja
Czym jest rekurencja? Gdy patrzymy w lustro, na które nakierujemy drugie – widzimy nieskończony ciąg odbić siebie samego. W matematyce i informatyce mamy do czynienia z rekurencją, gdy jakaś funkcja w swoim „wnętrzu” odwołuje się do siebie samej (takie przysłowiowe pudełko w pudełku). Dlaczego stosujemy rekurencję, skoro większość informatycznych problemów można by rozwiązać w sposób tradycyjny – iteracyjny? Po pierwsze jest to czasem bardziej naturalny sposób rozwiązania problemu, a po drugie zyskujemy zwięzły zapis problemu.

Co jest najważniejsze w rekurencji? Należy pamiętać o takim skonstruowaniu warunku zakończenia wywoływania funkcji wewnątrz nie samej, aby nie zapętliła się w nieskończoność, co może doprowadzić nawet do zawieszenia się systemu. W algorytmice metodą rekurencyjną realizowane są min: algorytm Euklidesa, ciąg Fibonacciego, wyszukiwanie binarne, sortowanie szybkie, sortowanie przez scalanie, zamiana z dziesiętnego na dowolny inny system liczbowy, przeszukiwanie w głąb, podnoszenie do potęgi, wypisanie wyrazu wspak, silnia i wiele innych.

Zadanie - Silnia
W matematyce silnię zapisujemy za pomocą wykrzyknika i tak 3! jest równe 1*2*3 = 6, co można informatycznie rozwiązać za pomocą pętli. Matematyczna (rekurencyjna) definicja silni:

• dla n = 0 silnia = 1

• dla n > 0 silnia = silnia(n-1) * n

Funkcję SILNIA definiujemy zgodnie z matematyczną definicją – dla wszystkich n większych od zera wywołujemy jeszcze raz funkcję z parametrem n-1.

long SILNIA(int n){
  if (n==0) return 1;
  else return n*SILNIA(n-1);
}
...
cout << "n=";
int k;
cin >> k;
cout << k << "!=" << SILNIA(k) << endl;

Zadanie - Euklides
Wyznaczamy największy wspólny dzielnik NWD dwóch liczb, czyli taką możliwie największą liczbę, która dzieli obie liczby. Wybieramy większą z dwóch liczb i zamieniamy ją na różnicę większej i mniejszej. Czynność tą powtarzamy do momentu uzyskania dwóch takich samych wartości.

long EUKLIDES(int a, int b){
  if (a!=b)
    if (a>b) return EUKLIDES(a-b,b);
    else return EUKLIDES(a,b-a);
  return a;
}
…
cout << "a= b= ";
int a,b;
cin >> a >> b;
cout << "NWD(" << a << "," << b << ")=" << EUKLIDES(a,b) << endl;

Zadanie – Fibbonaci
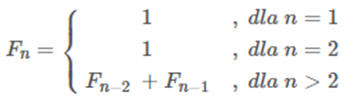
Ciąg Fibonacciego definiujemy następująco: pierwszy i drugi element ciągu są równe 1. Każdy następny otrzymujemy dodając do siebie dwa poprzednie. Matematycznie wygląda to następująco:

long FIBBONACI(int n){
  if (n<3) return 1;
  else return FIBBONACI(n-2) + FIBBONACI(n-1);
}
…
cout << "miesiące=";
int f;
cin >> f;
cout << "królików =" << FIBBONACI(f) << endl;

Zadanie - Wspak
Wczytujemy tekst z klawiatury. Po naciśnięciu klawisza ENTER tekst zostaje wypisany w kolejności odwrotnej.

• wczytujemy z klawiatury jeden znak GETCHAR

• jeżeli znak nie jest ENTERem, to

• rekurencyjnie wywołujemy funkcję ODWROTNIE

• wczytaj znak - gdy rekurencja się skończy – ENTER

• wyświetlane są znaki PRINTF, a kolejne zakończenia funkcji wyświetlą znaki od końca.

#include 
...
void ODWROTNIE(){
  char znak;
  znak=getchar();
  if (znak!='\n') {
    ODWROTNIE();
    printf("%c",znak);
  }
}

Zadanie - Horner
Każdy wielomian (np. f(-3)=3x^4 +7x^3=2x^2+10x-3) można zapisać w postaci: 

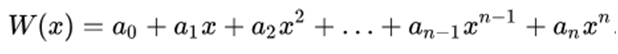
Jeśli chcemy obliczyć wartość tego wielomianu dla x=3, to należy wykonać 5 mnożeń. Jeśli rośnie stopień wielomianu, tych mnożeń będziemy musieli wykonać coraz więcej. Ponieważ operacja mnożenia jest dla przeciętnego komputera czasochłonna, dlatego poszukuje się metod, które obliczają wartość wielomianów z mniejszą liczbą mnożeń. Jednym z rozwiązań jest tzw. schemat Hornera

W programie współczynniki wielomianu zapisane są w tablicy WSP: w elemencie zerowym ostatni współczynnik (potęga 0), w pierwszym – 1, itd. Parametry funkcji HORNER:

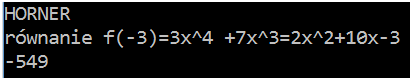• n – największa potęga wielomianu

• a[] – tablica ze współczynnikami

• x – argument wielomianu

Jeśli wielomian jest stopnia zerowego, to wynikiem jest komórka zerowa tablicy. W przeciwnym razie wykonujemy rekurencyjne mnożenie i dodajemy współczynnik z tablicy: Wn-1(x)*x + A[n]

double HORNER(int n, double a[], double x){
  if (n==0) return a[0];
  else return HORNER(n-1, a, x) * x + a[n];
}
…
int s=4;
double wsp[]={-3,10,-2,7,3};
double x=-3;
cout << HORNER(s,wsp,x) << endl;

Zadania

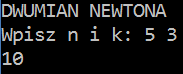1) Stosując rekurencję oblicz wartość dwumianu Newtona (n,k)=n!/(k!*(n-k)!)

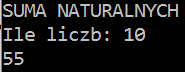2) Stosując rekurencję oblicz wartość sumy kolejnych liczb naturalnych suma(n)=n+suma(n-1)!

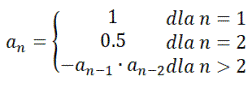
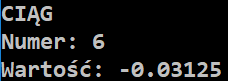3) Pewien ciąg opisany na poniższym obrazku generuje wyrazy w sposób rekurencyjny. Napisz program, który wyliczy wartość n-tego wyrazu ciągu.

4) Napisz program, który zapisze podaną liczbę dziesiętną w systemie dwójkowym. Rozwiąż zadanie rekurencyjnie.

5) Napisz program, który wyznaczy sumę cyfr liczby naturalnej z zakresu. Rozwiąż zadanie metodą rekurencyjną.

Przykładowe rozwiązania zadań
Jedynie ciężka umysłowa praca i zrozumienie działania programu może nauczyć programowania!

//zadanie 1
long SILNIA(int n){
	if (n==0) return 1;
	else return n*SILNIA(n-1);
}

long DWUMIAN(int n, int k){
	long w;
	w=SILNIA(n)/(SILNIA(k)*(SILNIA(n-k)));
	return w;
}

cout << "DWUMIAN NEWTONA" << endl;
int n,k;
cout << "Wpisz n i k: ";
cin >> n >> k;
cout << DWUMIAN(n,k) << endl;

//zadanie 2
long SUMA(int n){
	long w=1;
	if (n>1) w=n + SUMA(n-1);
	return w;
}
cout << "SUMA NATURALNYCH" << endl;
int ile;
cout << "Ile liczb: ";
cin >> ile;
cout << SUMA(ile) << endl;

//zadanie 3
double CIAG(int n){
	if(n==1) return 1;
	if(n==2) return 0.5;
	return -CIAG(n-1)*CIAG(n-2);
}

int n;
cout << "CIĄG" << endl;
cout << "Numer: ";
cin >> n;
cout << "Wartość: " << CIAG(n) << endl;		

//zadanie 4
void DECBIN(int liczba){
  if(liczba>0){
	DECBIN(liczba/2); 
	//rekurencyjnie dzielimy całkowicie przez dwa
	//reszta z dzielenia przez dwa - modulo 
	//wypisywana na ekranie od tyłu, np liczba 87
	// 87  43  21  10  5  2  1
	// 1   1   1   0   1  0  1
	cout << liczba % 2;
  }
}
int liczba;
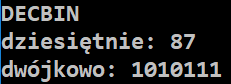
cout << "DECBIN" << endl;
cout << "dziesiętnie: ";
cin >> liczba;
cout << "dwójkowo: ";
DECBIN(liczba);
cout << endl;

//zadanie 5
//aby wyłuskać cyfrę wykonujemy %10 - modulo
// aby skrócić liczbę o jedną pozycję
//wykonujemy dzielenie całkowite przez 10
int SUMACYFR(long long n){
  if( n> 0)
    return n%10 + SUMACYFR(n/10);
  return 0;
}

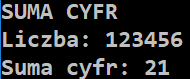
long long c;
cout << "SUMA CYFR" << endl;
cout << "Liczba: ";
cin >> c;
cout << "Suma cyfr: " << SUMACYFR(c) << endl;

//SZABLON
#include <stdlib.h>	//system
#include <iostream>	//cout
#include <iomanip>	//fixed
#include <cmath>	//pow
using namespace std;
int main(){
  setlocale(LC_ALL, "");


  system("pause");
}