Lekcja 10

Sortowanie w C++

1. naiwne
2. bąbelkowe
3. algorithm
4. scalanie
5. quicksort
6. własności
7. zadania
8. rozwiązania

Porządkowanie danych jest jedną z najczęściej wykonywanych operacji przez komputery. Po co się porządkuje dane? Po prostu w danych uporządkowanych szybciej się wyszukuje informacje! Warto więc poświęcić czas na porządkowanie, które zwykle wykonujemy jeden raz, by potem wiele razy szybko i sprawnie wśród nich wyszukiwać.

Dane do sortowania przechowujemy z reguły w tablicach. W języku C tablice przesyłane jako parametry funkcji, zawsze traktowane są jak referencje. Projektant C wymyślił tak, aby zmienne tablicowe zajmowały mniej miejsca w pamięci, ale…! Jednym z problemów jest to, że w C nie można w prosty sposób sprawdzić jak wielka jest tablica – ile ma elementów!

Sortowanie przez wybór (naiwne)
Sortowanie przez wybór jest naturalne. Szukamy w zbiorze liczb tej najmniejszej (największej) i ustawiamy ją na początku zbioru. Czynności szukania i wstawiania powtarzamy z pominięciem już uporządkowanego elementu.

Specyfikacja
Zadanie: uporządkuj rosnąco ciąg N liczb zapisanych w tablicy TN
Dane: tablica liczb TN Wynik: tablica liczb TN z uporządkowanymi liczbami
Algorytm:

1. i=0

2. znajdź minimum w ciągu liczb i..N-1

3. zamień w tablicy TN elementy TN[i] z TN[min]

4. zwiększ wartość i o 1

5. jeśli i < N-1 wróć do 2

void ZAMIANA(int &a, int &b){
  int p=a;
  a=b;
  b=p;
}

int MINIMUM(int poc,int kon,int t[]){
  int k=0;
  int mink=999999;
  for (int i=poc; i <= kon; i++)
    if (t[i] < mink){
      mink=t[i];
      k=i;
    }
  return k;
}

void PiszTablica(int n, int t[]){
  for (int i=0; i < n; i++){
    cout.width(4);
    cout << t[i];
  }
  cout << endl;
}

void SortNaiwne(int n, int t[]){
  int i=0;
  do{
    int min=MINIMUM(i,n-1,t);
    ZAMIANA(t[i],t[min]);
    i=i+1;
  } while (i < n-1);
}
...
const int N=20;
int tt[N];
srand(time(NULL));
for(int i = 0; i < N; i++) 
  tt[i] = rand() % 100;
PiszTablica(N,tt);
SortNaiwne(N,tt);
PiszTablica(N,tt);

Funkcja ZAMIANA zwraca zmienne "zamienione miejscami" - przekazujemy parametry przez referencję.

Funkcja MINIMUM przeszukuje tablicę od elementu poc do elementu kon. Jako parametr podajemy też całkowitą ilość elementów w tablicy t[].

W programie głównym deklarujemy tablicę tt[] o 20 komórkach ponumerowanych od 0 do 19. Inicjujemy licznik pseudolosowy, aby losowane były różne liczby po każdym uruchomieniu programu. Najpierw wypisujemy elementy nieposortowane, a potem posortowane.

Sortowanie bąbelkowe
Porównujemy parami dwie sąsiednie liczby, i jeśli pierwsza jest mniejsza od drugiej (lub większa), to zamieniamy je miejscami. Jednokrotna analiza tablicy przestawia najmniejszy element (największy) na początek (koniec). Tablicę trzeba więc analizować tyle razy ile jest elementów. Aby przyspieszyć sortowanie można pomijać elementy już uporządkowane.

Algorytm:

1. ustaw element początkowy na 0 i zwiększaj go o jeden aż osiągnie wartość N-1

2. ustaw element analizowany na 0 i zwiększaj go o 1 aż osiągnie wartość N-pocz-1

3. porównaj elementy tablicy i i i+1 i dokonaj ich zamiany gdy t[i] > t[i+1]

4. wróć do punktu 3

5. wróć do punktu 2

void SortBuble(int n, int t[]){
  for (int pocz=0; pocz < n-1; pocz++)
    for (int i=0; i < n-pocz-1; i++)
      if (t[i] > t[i+1])
        ZAMIANA(t[i],t[i+1]);
}
for(int i = 0; i < N; i++) 
	tt[i] = rand() % 100;
PiszTablica(N,tt);
SortBuble(N,tt);
PiszTablica(N,tt);

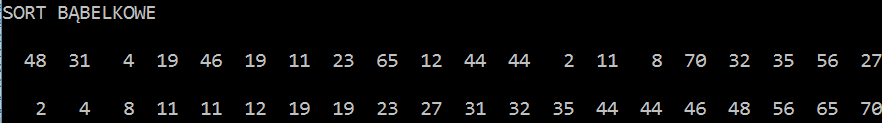
Biblioteka <algorithm>
Biblioteka algorithm posiada szereg gotowych algorytmów, m.in. algorytm sortowania. Funkcja SORT jest bardzo przydatna, gdyż nie musimy pisać kodu sortującego. W najprostszej postaci wystarczy podać nazwę tablicy i ilość elementów do posortowania. Nie ma też znaczenia, czy tablica zawiera liczby czy teksty.

#include <algorithm>
...
int tab[] = {9,8,7,0,8,6,3,1,7,2};
sort(tab, tab+10);

Sortowanie z własnym porównaniem
Standardowo funkcja SORT porządkuje liczby rosnąco. Jeśli chcemy posortować liczby w inny sposób, np. malejąco musimy przygotować odpowiednią funkcję.

bool porownaj(int a, int b){
	return a > b;
}
...
sort(tab, tab+10, porownaj);

Sortowanie przez scalanie (http://www.home.umk.pl)
W algorytmie sortowania przez scalanie jest wykorzystywana strategia "dziel i zwyciężaj". Wyobraźmy sobie, że mamy już dwa uporządkowane ciągi, a chcemy utworzyć z nich jeden – także uporządkowany. Można oczywiście połączyć i posortować jedną ze znanych metod, ale nie zostanie wykorzystane uporządkowanie obu ciągów. Można zastosować następujący sposób:

• porównujemy ze sobą pierwsze elementy z każdego z ciągów danych.

• mniejszy element wstawiamy do nowego ciągu i usuwamy z ciągu danych.

• powtarzamy te czynności, aż oba ciągi danych będą puste.

W ten sposób, w nowo utworzonym ciągu wszystkie elementy są uporządkowane, a co najważniejsze operacja ta wymaga wykonania niewielu porównań. Wiadomo już, jak z dwóch uporządkowanych ciągów otrzymać jeden. Wykorzystując to, można sformułować algorytm sortowania dowolnego ciągu:

• podziel ciąg na dwie równe części (jeśli ciąg ma nieparzystą liczbę elementów, jedna z części będzie miała o jeden element więcej).

• każdą z części uporządkuj.

• połącz dwa uporządkowane ciągi w jeden ciąg uporządkowany.

Pozostaje jeszcze rozstrzygnąć, w jaki sposób posortować każdy z dwóch podciągów? W odpowiedzi zawiera się cała siła tego algorytmu: w ten sam sposób! Po prostu wywołujemy rekurencyjnie ten sam algorytm dla każdego z podciągów. Aby takie postępowanie nie przebiegało w nieskończoność należy określić, kiedy zaprzestajemy podziału ciągu. Następuje to, gdy sortowany ciąg ma mniej niż dwa elementy. Ostatecznie algorytm ma następującą postać:

• Jeśli ciąg zawiera więcej niż jeden element, to podziel go na dwie równe części (lub prawie równe, jeśli ciąg ma nieparzystą liczbę elementów).

• Posortuj pierwszą część stosując ten sam algorytm.

• Posortuj drugą część stosując ten sam algorytm.

• Połącz dwa uporządkowane ciągi w jeden ciąg uporządkowany.

const int N = 20;
int d[N], p[N];

void MergeSort(int i_p, int i_k)
{
  int i_s,i1,i2,i;
  i_s = (i_p + i_k + 1) / 2;
  if (i_s - i_p > 1) MergeSort(i_p, i_s - 1);
  if (i_k - i_s > 0) MergeSort(i_s, i_k);
  i1 = i_p; i2 = i_s;
  for (i = i_p; i <= i_k; i++)
    p[i] = ((i1 == i_s) || ((i2 <= i_k) &&
    (d[i1] > d[i2]))) ? d[i2++] : d[i1++];
  for(i = i_p; i <= i_k; i++) d[i] = p[i];
}

...  
for(i = 0; i < N; i++) d[i] = rand() % 100;
for(i = 0; i < N; i++) cout << setw(4) << d[i];
cout << endl;

MergeSort(0,N-1);

for(i = 0; i < N; i++) cout << setw(4) << d[i];
cout << endl;

Sortowanie Szybkie QuickSort (eduinf.waw.pl)
W przypadku tej metody sortowania jest wykorzystywana strategia "dziel i zwyciężaj". Przypuśćmy, że potrafimy podzielić dany ciąg na dwie takie części, że elementy pierwszego ciągu są mniejsze od elementów drugiego ciągu, czyli nieformalnie mówiąc, na elementy "małe" i "duże". Mając taki podział ciągu, możemy każdą z części uporządkować osobno. Otrzymamy ciąg składający się z uporządkowanych elementów "małych", a po nich następują uporządkowane elementy "duże" - czyli cały ciąg jest już uporządkowany!

Idea sortowania szybkiego jest następująca:

• DZIEL: najpierw sortowany zbiór dzielimy na dwie części w taki sposób, aby wszystkie elementy leżące w pierwszej części (zwanej lewą partycją) były mniejsze lub równe od wszystkich elementów drugiej części zbioru (zwanej prawą partycją).

• ZWYCIĘŻAJ: każdą z partycji sortujemy rekurencyjnie tym samym algorytmem.

• POŁĄCZ: połączenie tych dwóch partycji w jeden zbiór daje w wyniku zbiór posortowany.

Do utworzenia partycji musimy ze zbioru wybrać jeden z elementów, który nazwiemy piwotem. W lewej partycji znajdą się wszystkie elementy niewiększe od piwotu, a w prawej partycji umieścimy wszystkie elementy niemniejsze od piwotu. Położenie elementów równych nie wpływa na proces sortowania, zatem mogą one występować w obu partycjach. Również porządek elementów w każdej z partycji nie jest ustalony. Jako piwot można wybierać element pierwszy, środkowy, ostatni, medianę lub losowy.

Dla naszych potrzeb wybierzemy element środkowy. Dzielenie na partycje polega na umieszczeniu dwóch wskaźników na początku zbioru - i oraz j. Wskaźnik i przebiega przez zbiór poszukując wartości mniejszych od piwotu. Po znalezieniu takiej wartości jest ona wymieniana z elementem na pozycji j. Po tej operacji wskaźnik j jest przesuwany na następną pozycję. Wskaźnik j zapamiętuje pozycję, na którą trafi następny element oraz na końcu wskazuje miejsce, gdzie znajdzie się piwot. W trakcie podziału piwot jest bezpiecznie przechowywany na ostatniej pozycji w zbiorze.

const int N = 20;
int d[N];

void QuickSort(int lewy, int prawy){
  int i,j,piwot;
  i = (lewy + prawy) / 2;
  piwot = d[i]; 
  d[i] = d[prawy];
  fo r(j = i = lewy; i < prawy; i++)
  if (d[i] < piwot){
    swap(d[i], d[j]);
    j++;
  }
  d[prawy] = d[j]; 
  d[j] = piwot;
  if (lewy < j - 1)  QuickSort (lewy, j - 1);
  if (j + 1 < prawy) QuickSort (j + 1, prawy);
}
...  

for(i = 0; i < N; i++) d[i] = rand() % 100;
for(i = 0; i < N; i++) cout << setw(4) << d[i];
cout << endl;

QuickSort(0,N - 1);

for(i = 0; i < N; i++) cout << setw(4) << d[i];
cout << endl;

O algorytmach teoretycznie - własności algorytmów
Analiza algorytmów jest zadaniem złożonym. Jeśli piszemy jakiś algorytm, to powinien być napisany precyzyjnie i szczegółowo, aby można go było zrozumień i przekształcić na konkretny język programowania. Najważniejsze własności algorytmów

1. poprawność – rozwiązuje problem zgodnie ze specyfikacją (dane i wyniki)

2. skończoność – gwarantuje uzyskanie wyniku w skończonym czasie

3. złożoność – skończony czas i określone zasoby komputera (pamięć i szybkość)

4. efektywność - otrzymam y rozwiązanie w możliwie najkrótszym czasie bez błędów

Zadania

1) W zmiennej tekstowej znajduje się zestaw losowych znaków A..Z. Posortuj go wykorzystując funkcje sortujące z lekcji.

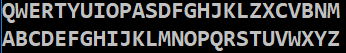
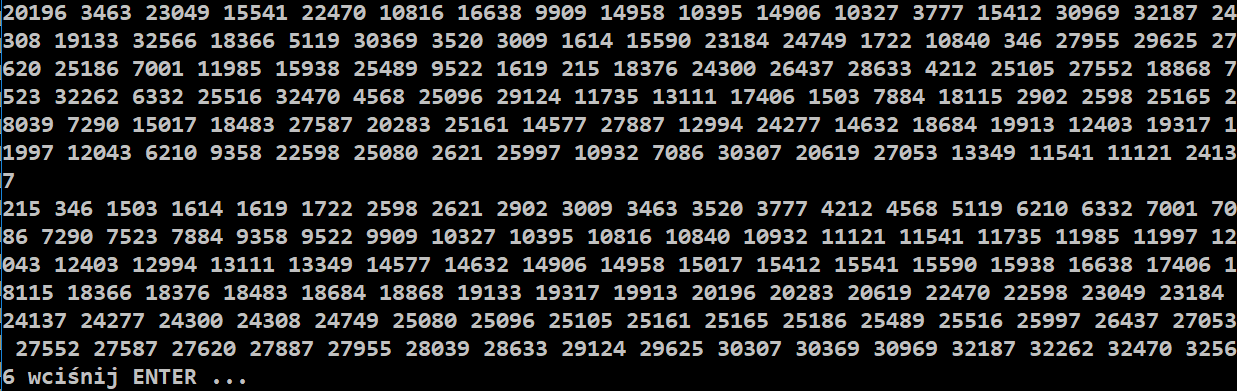
2) Zapisz do pliku tekstowego 100 losowych liczb. Następnie go wczytaj, liczby z pliku posortuj i zapisz w pliku z nazwą wpisaną z klawiatury.

3) Zmienna zawiera tekst, np. treść tego zadania. Policz ile jest każdego ze znaków alfabetu i posortuj je malejąco. Wyniki na ekranie i w pliku tekstowym.

przed po

4) Wygeneruj plik tekstowy dwojkowe.txt zawierający 100 losowych ciągów zer i jedynek - 2..8 bitów. Wczytaj plik do programy, zamień liczby dwójkowe na dziesiątkowe i posortuj malejąco.

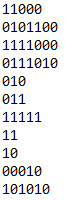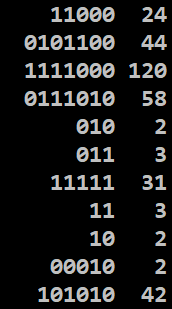plik przed po

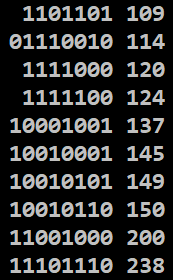
5) Wygeneruj plik tekstowy daty.txt zawierający losowe daty w formacie RRRR-MM-DD. Lata w przedziale 1918..2018. Wczytaj plik do programu i posortuj daty.

plik 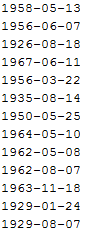przed po

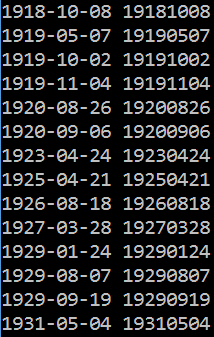
Przykładowe rozwiązania zadań
Jedynie ciężka umysłowa praca i zrozumienie działania programu może nauczyć programowania!

//zadanie 1
//zamienimy znaki na kody (liczby) w tablicy 
string ZNAKI="QWERTYUIOPASDFGHJKLZXCVBNM";
int dl=ZNAKI.length();
int KODY[dl];
for (int i=0; i < dl; i++){
  KODY[i]=int(ZNAKI[i]);
}
//sortowanie
SortNaiwne(dl,KODY);
//ale teraz trzeba odtworzyc znaki
string z="";
for (int i=0; i < dl; i++){
  z=z+char(KODY[i]);
}
cout << ZNAKI << endl;
cout << z << endl;

//zadanie 2
//zapisanie do pliku
ofstream zad2("zad2.txt");
for (int i=1; i <= 100; i++){
	int l=rand();
	zad2 << l << endl;
}
zad2.close();
//odczytanie do tablicy 100 liczb
ifstream zad2o("zad2.txt");
int TA[100];
int i=0;
while (!zad2o.eof()){
	zad2o >> TA[i];
	i++;
}
zad2o.close();
//sprawdzone - czyta z pliku dobrze
for (int i=0; i < 100; i++)
  cout << TA[i] << " ";
//sortowanie
SortNaiwne(100,TA);
cout << endl;
for (int i=0; i < 100; i++)
  cout << TA[i] << " ";

//zadanie 3
string zdanie="Zmienna zawiera tekst, np. treść tego zadania. Policz ile jest każdego ze znaków alfabetu i posortuj je malejąco. Wyniki na ekranie i w pliku tekstowym.";
//tablica na kody znaków i liczniki znaków
//po sortowaniu musimy odtworzyć kody 
//kod znaku w zerowej kolumnie 
//liczniki są w pierwszej kolumnie
//kody do kolumny 0 i zerowanie kolumny 1
int Z[256][2];
for (int i=0; i < 256; i++){
  Z[i][0]=i;//kod znaku
  Z[i][1]=0;//licznik znaków
}
int d=zdanie.length();
//policzenie znaków w zdaniu
//liczniki w kolumnie 1
for (int i=0; i < d; i++){
  int kod=int(zdanie[i]);
  Z[kod][1]++;
}
//wypisanie liczników, jeśli były jakieś znaki policzone
for (int i=0; i < 256; i++)
  if (Z[i][1] > 0)
    cout << i << " " << char(Z[i][0]) << " " << Z[i][1] << endl;
//nie mozna posortować sposobem z lekcji bo tablica jednowymiarowa
//trzeba napisać sortowanie od nowa
//bąbelkowe
for (int pocz=0; pocz < 255; pocz++)
	for (int i=0; i < 255-pocz; i++)
		if (Z[i][1] > Z[i+1][1]){
			int p[2];
      p[0]=Z[i][0];
      p[1]=Z[i][1];
			Z[i][0]=Z[i+1][0];
			Z[i][1]=Z[i+1][1];
			Z[i+1][0]=p[0];
			Z[i+1][1]=p[1];
		}
//posortowane
cout << endl;
for (int i=0; i < 256; i++)
  if (Z[i][1] > 0)
    cout << int(Z[i][0]) << " " << char(Z[i][0]) << " " << Z[i][1] << endl;

//zadanie 4
//tworzymy plik z liczbami dwójkowymi
ofstream NDzapis("dwojkowe.txt");
int ile;
int znak;
for (int j=1; j <= 100; j++){
	//2-8 bitów
	ile=rand() %7 +2; 
	string napis="";
	for (int i=1; i <= ile; i++){
		//0 lub 1 losowo
    		znak=rand() % 2;
		//znak ASCII '0' lub '1'
		napis=napis+char(znak+48); 
	}
	NDzapis << napis;
	//końce wierszy bez ostatniej linii
	if (j < 100) NDzapis << endl;
}
NDzapis.close();

//wczytujemy do tablicy 
//nie musimy zerować bo bedzie wypełniona 
string DWO[100];
ifstream NDodczytA("dwojkowe.txt");
string nap;
int l=0;
while (!NDodczytA.eof()){
	NDodczytA >> nap;
	DWO[l]=nap;
	l++;
}
NDodczytA.close();

//zamieniamy na dziesiętne do innej tablicy
int DZI[100];
for (int i=0; i < 100; i++){
  //dwójkowy napis
  string dwo=DWO[i];
  int d=dwo.length();
  int dzi=0;
  //przelatujemy po znakach napisu
  //od zera ale potęga na odwrót
  for (int j=0; j < d; j++){
    //znak zamieniony na liczbę 0 lub 1
    int licz=int(dwo[j])-48;
    //wyliczamy wagę cyfry
    int waga=licz*pow(2,d-j-1);
    //sumujemy wagi - dziesiętna
    dzi=dzi+waga;
  }
  DZI[i]=dzi;
}

//wypisanie na ekran nieposortowanych
for (int i=0; i < 100; i++){
  cout.width(9);
  cout << DWO[i];
  cout.width(4);
  cout << DZI[i] << endl;
}

//sortujemy
//napisać sortowanie od początku i sortować obie tablice
//bąbelkowe
for (int pocz=0; pocz < 99; pocz++)
	for (int i=0; i < 99-pocz; i++)
		if (DZI[i] > DZI[i+1]){
			int p=DZI[i];
      			string q=DWO[i];
      			DZI[i]=DZI[i+1];
			DWO[i]=DWO[i+1];
			DZI[i+1]=p;
			DWO[i+1]=q;
	 	}

//wypisanie
cout << endl;
for (int i=0; i < 100; i++){
  cout.width(9);
  cout << DWO[i];
  cout.width(4);
  cout << DZI[i] << endl;
}	

//zadanie 5
//konwertujemy liczba-tekst za pomocą strumieni
//datę w formacie RRR-MM-DD produkujemy z kawałków napisów
ofstream DATYzapis("daty.txt");
for (int i=1; i <= 100; i++){
	string data="";
	//daty 1918-2018
  	int rok=rand() % 101 +1918; 
	//date na liczbę za pomocą strumieni! - lekcja 7
  	stringstream srok;
	srok << rok;
  	string trok=srok.str();	
	//w identyczny sposób miesiąc i dzień
	int mie=rand() % 12 +1; 
	stringstream smie;
  	smie << mie;
  	string tmie=smie.str();	
  	if (mie < 10) tmie='0'+tmie;
  	int dzi=rand() % 30 +1; 
	stringstream sdzi;
  	sdzi << dzi;
  	string tdzi=sdzi.str();	
  	if (dzi < 10) tdzi='0'+tdzi;
  
  	data=trok+'-'+tmie+'-'+tdzi;
  	DATYzapis << data;
	//końce wierszy bez ostatniej linii
	if (i < 100) DATYzapis << endl;
}
DATYzapis.close();

//wczytujemy daty z pliku do tablicy napisów
string DAT[100];
ifstream DATYodczyt("daty.txt");
string dat;
int l=0;
while (!DATYodczyt.eof()){
	DATYodczyt >> dat;
	//data w postaci tekstu
	DAT[l]=dat;
	l++;
}
DATYodczyt.close();

//jak posortować nie korzystają z gotowych funkcji bibliotecznych
//zamieniamy datę na liczbę "doklejając" RRRRMMDD
//konwersja za pomocą atoi i c_str()
int DATL[100];
for (int i=0; i < 100; i++){
	//z napisu w tablicy DAT wycinamy 4 pierwsze znaki RRRR
	string rr=DAT[i].substr(0,4);
	string mm=DAT[i].substr(5,2);
	string dd=DAT[i].substr(8,2);
	//funkcja c_str() konwertuje string na char
	//i wtedy można stosować atoi - brrr
	int rrr=atoi(rr.c_str());
	int mmm=atoi(mm.c_str());
	int ddd=atoi(dd.c_str());
	int datl=rrr*10000+mmm*100 + ddd;
	DATL[i]=datl;
	//daty i liczby na ekran
	cout << DAT[i] << " " << DATL[i] << endl;
}
	
//sortowanie osobno po DATL
//bąbelkowe
for (int pocz=0; pocz < 99; pocz++)
	for (int i=0; i < 99-pocz; i++)
		if (DATL[i] > DATL[i+1]){
			int p=DATL[i];
			string q=DAT[i];
			DATL[i]=DATL[i+1];
			DAT[i]=DAT[i+1];
			DATL[i+1]=p;
			DAT[i+1]=q;
	 }
//na ekran po sortowaniu
for (int i=0; i < 100; i++)
	cout << DAT[i] << " " << DATL[i] << endl;

//SZABLON
#include <stdlib.h> //system
#include <iostream> //cout
#include <iomanip> //fixed
#include <cmath> //pow
#include <fstream> //ofstream
#include <sstream> //stringstream 

using namespace std;
int main(){
  setlocale(LC_ALL, "");
  //licznik pseudolosowy
  srand(time(NULL));
 

  system("pause");
}