mgr inż. Wacław Libront * Bobowa 2017-2019

ZSO Bobowa, ul. Długoszowskich 1, 38-350 Bobowa, tel: 0183514009, fax: 0183530221, email: sekretariat@zsobobowa.eu, www: zsobobowa.eu

Lekcja 4

Rekurencja w JS

  1. rekurencja
  2. drzewa
  3. Koch

Czym jest rekurencja? Takie „pudełko w pudełku, w pudełku…”. W funkcji rekurencyjnej musi być „strażnik”, którego zadaniem jest zakończenie wywoływania kolejnych funkcji – odkrywania kolejnych pudełek. Bez strażnika program będzie wykonywał się w nieskończoność, co grozi zawieszeniem się programu.

Kwadrat rekurencyjny
Funkcja rysuje kwadraty, ale nie za pomocą poznanej pętli FOR, ale przez kolejne wywołanie samej siebie. Funkcja najpierw "otwiera" kolejne "pudełka", i gdy dojdzie do ostatniego (n=1) zaczyna je zamykać, i podczas zamykania rysowany jest kwadrat z odpowiednimi parametrami.

Dla zobrazowania różnicy utworzono podobną funkcję działającą w pętli.

<canvas width="400" height="400" id="can"></canvas>
<script>
  var c = can.getContext("2d");

// funkcja tradycyjna
function nKwadrat(n) {
  c.strokeStyle = "blue";
  for (var i = n; i > 0; i = i - 1) {      
    c.strokeRect(i * 30, i * 30, 100, 100);
  }
}
//uruchomienie
nKwadrat(4);

// funkcja rekurencyjna
function nKwadratR(n) {  
  if (n > 1) {
    nKwadratR(n - 1);
  }
  c.strokeRect(n * 30, n * 30, 100, 100);
}
//uruchomienie
nKwadratR(4)

</script>

Drzewa
Drzewa są typowym przykładem rekurencyjnego rysowania. Pojedyncza gałąź jest zwykłym cienkim prostokątem. Jak narysować Drzewo? Najpierw obracamy układ i rysujemy cienki prostokąt. Następnie sprawdzamy czy długość gałęzi nie przekroczyła zakładanego minimum i przesuwamy układ na koniec narysowanego prostokąta. Teraz rekurencyjnie wywołujemy rysowanie dwóch pochylonych w różne strony gałęzi. Otrzymamy drzewo dokładnie symetryczne. Jeśli wprowadzimy odrobinę chaosu za pomocą losowego kąta obrotu…? 

//drzewa
var kat = 0.35;
var Skala = 0.75;
var l = 75;
var minL = 5;
var w = c.canvas.width;
var h = c.canvas.height;
c.translate(w/2, h);
rysujGalaz(l, 0);

function rysujGalaz(l, kierunek) {
  c.save();
  //losowy kąt jesli chcemy rozne drzewa
  kat=(Math.random()*60)*Math.PI/180;
  c.rotate(kat * kierunek);
  c.fillRect(-l / 20, 0, l / 10, -l);
  if (l > minL) {
    c.translate(0, -l);
    rysujGalaz(l * Skala, -1);
    rysujGalaz(l * Skala, 1);
  }
  c.restore();
}

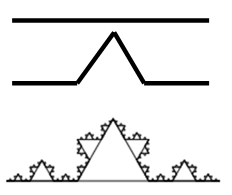Płatek Kocha
Płatek składa się z jednej linii. Jeśli długość linii jest mniejsza od 5, to rekurencyjnie rysowane są 4 linie w układzie z "wybojem" (kąty 60°). I to wystarczy, aby narysować płatek Kocha.

Płatek można powtórzyć trzy razy, za każdym razem przesuwając się o długoć podstawowego boku płatka i obracając o 120 stopni - powstanie "seretka".

c.translate(100,100);
function platek(bok){
  c.save();
  c.beginPath();      //linia
  c.moveTo(0,0);
  c.lineTo(bok,0);
  c.stroke();
  if (bok>5) {
    var b=bok/3;
    platek(b);
    c.translate(b,0);
    c.rotate(-60*Math.PI/180);
    platek(b);
    c.translate(b,0);
    c.rotate(120*Math.PI/180);
    platek(b);
    c.translate(b,0);
    c.rotate(-60*Math.PI/180);
    platek(b);
  }
  c.restore();
}

//płatek Kocha
platek(200);
//serwetka Kocha
for (var i=0;i<3;i++){
  platek(200);
  c.translate(200,0);
  c.rotate(120*Math.PI/180);  
}

Szablon

<canvas width="400" height="400" id="can"></canvas>
<script>
  var c = can.getContext("2d");



</script>