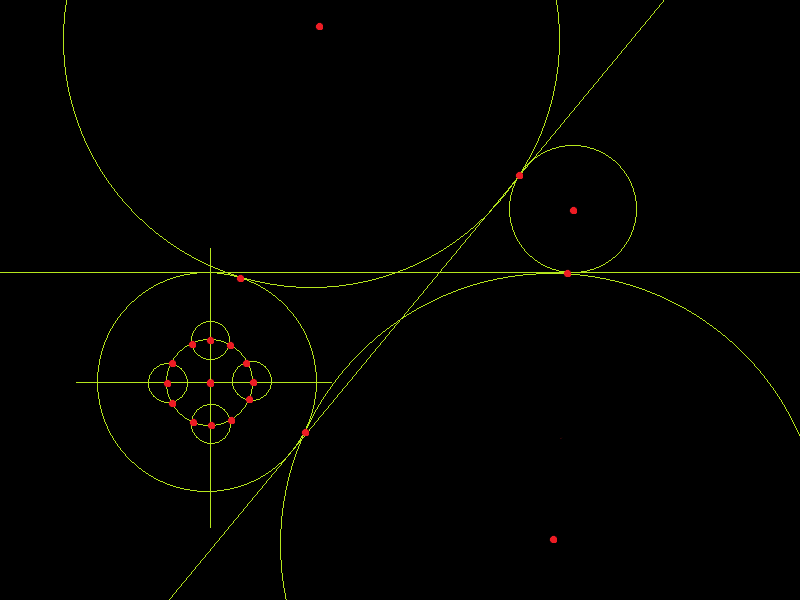
Niepozorny układ kresek i kółek, a w tle skomplikowany aparat matematyczny, pozwalający obliczać punkty przecięć i styczności geometrycznych obiektów. Po co to wszystko? Tych informacji potrzebuje każdy inżynier, który programuje obrabiarki, które to wykonują wszystkie te cudowne przedmioty, bez których nie wyobrażamy sobie codziennego życia. 1500 wierszy kodu w Pascalu, prawie 45000 znaków umożliwia dokonanie przeliczeń geometrycznych w celu znalezienia współrzędnych punktów na podstawie zdefiniowanej konfiguracji elementów podstawowych, jak: punkty linie i okręgi.
W czasach, gdy komputery torowały sobie drogę do przemysłu, gdy standardem była klawiatura i monochromatyczny monitor (jednokolorowy), gdy słowo "windows" jeszcze nikomu nie kojarzyło się z dzisiejszymi systemami operacyjnymi, czyli w roku 1990 istniały już co prawda programy do projektowania (CAD) lecz były bardzo drogie i niedostępne w krajach tzw. bloku państwa socjalistycznych. Mój program POG z roku 1990, który powstał w wojskowych Zakładach Mechanicznych w Tarnowie próbuje załatać tę dziurę.
Definiowanie konfiguracji, czyli rysowanie punktów, linii i okręgów odbywa się za pomocą trzyliterowych kodów wpisywanych z klawiatury:
- PXY-punkt we wspolrzednych prostokatnych X i Y
- PRQ-punkt we wspolrzednych biegunowych R i Q
- PLC-punkt przeciecia prostej L i okregu C
- PLL-punkt przeciecia dwoch prostych L1 i L2
- PCC-punkt przeciecia dwoch okregow C1 i C2
- PSC-punkt jako srodek okregu C
- PLI-zbior punktow na prostej
- PCR-zbior punktow na okregu
- TRA-zbior punktow jako przesuniecie rownolegle
- ROT-zbior punktow po obrocie
- SYM-zbior punktow jako odbicie symetryczne
- LPP-prosta przechodzaca przez dwa punkty P1 i P2
- LPC-prosta przechodzaca przez punkt P styczna do okregu C
- LLD-prosta odlegla od prostej L o odleglosc D
- LPQ-prosta przechodzaca przez punkt P tworzaca z prosta kat Q
- LCQ-prosta styczna do okregu C tworzaca z osia X kat Q
- LCC-prosta styczna do dwoch okregow C1 i C2
- CPR-okrag o srodku w punkcie P i promieniu R
- CPL-okrag styczny do prostej L przechodzacy przez punkt P
- CLL-okrag styczny do dwoch prostych L1 i L2
- CPP-okrag przechodzacy przez dwa punkty P1 i P2
- CLC-okrag styczny do prostej L i okregu C
- CCC-okrag styczny do dwoch okregow C1 i C2
- CPC-okrag przechodzacy przez punkt P styczny do okregu C
Dodatkowo zdefiniowano szereg funkcji specjalnych
- THH-wywolanie ekranu pomocy
- TSA-zapis danych na dysk
- TLO-odczyt z dysku zbioru z danymi
- TDD-wydruk wspolrzednych
- TWW-dane do dziurkowania na dysk ($)
- TSS-przesuwanie i skalowanie ekranu
- TPP-odleglosc miedzy dwoma punktami
- TTT-wspolrzedne pojedynczego elementu
- TRR-wyzerowanie danych
- T**-wyjscie do systemu operacyjnego
- TNP(L,C)-zmiana numeracji
- TBP(L,C)-wywolanie danych z bufora
- TMP(L,C)-wywolanie danych z tablicy glownej
- <F11>-numeracja wszystkich elementow
- <F12>-wywolanie ostatniego bufora
- <F13>-wywolanie ostatniej tablicy
- <F14>-skalowanie rysunku
- <F16> lub TCM-tryb kolorowy<>tryb jednobarwny.
Do komputera, który miałem wtedy do dyspozycji podpięty był ploter i drukarka, więc program potrafił rysować rysunki i drukować zestawy znalezionych punktów. Można też było „wydziurkować” układ punktów na specjalnej dziurkarce – taką taśmę „wciągała” obrabiarka sterowana numerycznie i była gotowa do wiercenia, frezowania, wycinania…
Wygenerowany tak rysunek można było zapisać na dysku w postaci pliku tekstowego (fragment poniżej):
FYJ22.RYS
P 0 0.0000000000E+00 0.0000000000E+00
P 1 4.9500000000E+02 0.0000000000E+00
P 2 -5.5000000000E+01 -5.9551298552E+01
P 3 -5.5000000000E+01 2.2781745931E+01
P 4 -3.2636360562E+01 -7.8566754695E+01
...
L 1 -6.7090909091E+00 -8.0721670567E+01
L 2 -5.7275649276E+01 -5.7275649276E+01
L 3 -5.5000000000E+01 0.0000000000E+00
L 4 -3.8890872965E+01 3.8890872965E+01
L 5 0.0000000000E+00 5.5000000000E+01
...
C 1 4.9500000000E+02 0.0000000000E+00 1.2200000000E+02
C 2 0.0000000000E+00 0.0000000000E+00 8.1000000000E+01
C 3 0.0000000000E+00 0.0000000000E+00 5.5000000000E+01
C 4 -3.1808043750E+01 -6.8601119178E+01 1.0000000000E+01
C 5 4.5000000000E+02 0.0000000000E+00 6.8000000000E+01
C 6 4.9500000000E+02 0.0000000000E+00 6.8000000000E+01
...
Cały (prawie) program dla zainteresowanych
Wacław Libront
Przykładowy fragment programu - obliczenia geometryczne:
unit procpog;
interface
var r0,r1,r2,r6,r7,a,a2,a3,a6,a7,a8,a9,b,b0,b1,b2,b6,b7,b8,b9,s1,s2,v1,v2,v9,
w,w1,n,no,n1,x,y,x1,x2,x6,x7,y1,y2,z,u1,u2,u3,u4,d,d3:real;
ktory,e1,m,m1,m2,m3,p,p0,j,j1,j2,j3,j4,j5,j6,j7,j8:byte;
blad:boolean;
tabp:array[0..255,1..2] of real; {tablica punktow}
tabl:array[0..255,1..2] of real; {tablica linii }
tabc:array[0..255,1..3] of real; {tablica okregow}
const liczba_max=9.0e30;
liczba_min=1E-5;
{PROCEDURY OBLICZAJACE WSPOLRZEDNE PLC}
procedure qqq(q:byte);
procedure ggg(j:byte);
procedure hhh(j:byte);
procedure bbb(j:byte);
procedure fff(j7:byte);
procedure eee(j6:byte);
procedure aaa(j8:byte);
procedure ccc(j4:byte);
procedure ddd(j5:byte);
procedure iii(j:byte);
procedure jjj(var m:byte);
procedure zzz(i,e1:byte);
implementation
procedure qqq(q:byte);
begin blad:=true end;
procedure ggg(j:byte);
begin
if tabl[j,1]>=(liczba_max/10)
then begin x1:=0;y1:=0;
z:=tabl[j,2];
if z=90 then begin u1:=0;u2:=1; exit end;
u1:=cos(z);
u2:=sin(z)
end
else begin x1:=tabl[j,1];
y1:=tabl[j,2];
u1:=-y1;
u2:=x1
end
end;
procedure hhh(j:byte);
begin x:=(x1*u2*u2-u1*u2*y1)/(u2*u2+u1*u1);
y:=(y1*u1*u1-u1*u2*x1)/(u2*u2+u1*u1);
if sqrt(x*x+y*y)>=d
then begin tabl[j,1]:=x;tabl[j,2]:=y end
else begin x:=liczba_max;
if abs(u1)liczba_min
then begin tabp[j,1]:=u1*(w1/w)+x1;
tabp[j,2]:=u2*(w1/w)+y1
end
else qqq(6)
end;
procedure fff(j7:byte);
begin if sqrt(sqr(x1-x2)+sqr(y1-y2))1) and (m<>2)
then if abs(y1-y2)>0
then if (((y1-y2)<0) and (m=3)) or (((y1-y2)>0) and (m=4))
then begin tabp[j7,1]:=x1;tabp[j7,2]:=y1;exit end
else begin tabp[j7,1]:=x2;tabp[j7,2]:=y2;exit end
else begin qqq(2); exit end;
if abs(x1-x2)>d
then if (((x1-x2)<0) and (m=1)) or (((x1-x2)>0) and (m=2))
then begin tabp[j7,1]:=x1;tabp[j7,2]:=y1;exit end
else begin tabp[j7,1]:=x2;tabp[j7,2]:=y2;exit end
else qqq(3)
end;
procedure eee(j6:byte);
begin if (tabp[j1,1]=0) and (tabp[j2,1]=0)
and (tabp[j1,2]=0) and (tabp[j2,2]=0) then qqq(3)
else
if (abs(tabp[j1,1]-tabp[j2,1])>d) or (abs(tabp[j1,2]-tabp[j2,2])>d)
then begin x1:=tabp[j1,1];y1:=tabp[j1,2];
u1:=tabp[j2,1]-tabp[j1,1];
u2:=tabp[j2,2]-tabp[j1,2];
hhh(j6)
end
else qqq(3)
end;
procedure aaa(j8:byte);
begin if v9<>1 then ggg(j1);
s1:=x1;s2:=y1;v9:=0;
x1:=(-u2)*a/(sqrt(u1*u1+u2*u2));
y1:=u1*a/(sqrt(u1*u1+u2*u2));
x2:=-x1;y2:=-y1;
fff(254);
if blad=true then exit;
x1:=s1+tabp[254,1];
y1:=s2+tabp[254,2];
hhh(j8)
end;
procedure ccc(j4:byte);
begin if v9<>1 then begin ggg(j1);
a9:=tabc[j2,1];b9:=tabc[j2,2];r0:=tabc[j2,3]
end;
a8:=x1;b8:=y1;
b:=u1*(x1-a9)+u2*(y1-b9);
b0:=b*b-(u1*u1+u2*u2)*(sqr(x1-a9)+sqr(y1-b9)-r0*r0);
if (b0<0) and ((abs(b0/(u1*u1+u2*u2)))>d)
then begin qqq(3); exit end;
b1:=(-b-sqrt(abs(b0)))/(u1*u1+u2*u2);
b2:=(-b+sqrt(abs(b0)))/(u1*u1+u2*u2);
x1:=u1*b1+a8;y1:=u2*b1+b8;
x2:=u1*b2+a8;y2:=u2*b2+b8;
fff(j4);
v9:=0
end;
procedure ddd(j5:byte);
begin a7:=tabc[j1,1];b7:=tabc[j1,2];r7:=tabc[j1,3];
a6:=tabc[j2,1];b6:=tabc[j2,2];r6:=tabc[j2,3];
d3:=sqrt(sqr(a7-a6)+sqr(b7-b6));
if d3>d
then begin d3:=(-(r7*r7)+r6*r6+a7*a7-(a6*a6)+b7*b7-(b6*b6))/(2*d3*d3);
u1:=-(b7-b6);u2:=a7-a6;
x1:=(a7-a6-b7+b6)*d3;
y1:=(a7-a6+b7-b6)*d3;
a9:=a7;b9:=b7;r0:=r7;
v9:=1;
ccc(j5)
end
else qqq(3)
end;
procedure iii(j:byte);
begin tabc[j,1]:=tabc[j1,1];
tabc[j,2]:=tabc[j1,2];
tabc[j,3]:=tabc[j1,3]+a*(-ord(m=5)+ord(m=6))
end;
procedure jjj(var m:byte);
begin x1:=tabp[251,1];y1:=tabp[251,2];
x2:=tabp[252,1];y2:=tabp[252,2];
if abs(y1-y2)<=d
then if x1<=(x2-d)
then m:=4*ord(m=1)+3*ord(m=2)
else m:=3*ord(m=1)+4*ord(m=2)
else if y1<=(y2-d)
then exit
else m:=ord(m=2)+2*ord(m=1)
end;
procedure zzz(i,e1:byte);
begin
tabc[e1,1]:=tabp[i,1];
tabc[e1,2]:=tabp[i,2]
end;
end.