Od tysięcy lat wpatrywaliśmy się w niebo, a dopiero od 300 rozumiemy jak i dlaczego się to wszystko kręci. Kto uczył się pilnie fizyki wie, że to wszystko dzięki grawitacji i dzięki wielkiemu „BUM”, które wydarzyło się prawie 14 miliardów lat temu. Dawni uczeni poświęcali lata swojego życia na obserwacje i żmudne obliczenia. Dzisiaj dzięki komputerom i prostej aplikacji GRAWILAB napisanej w Excelu możemy symulować ruchy planet oraz badać ich wzajemne oddziaływania.
Jak to można obliczyć i pokazać? Podstawowego równania dostarczył Newton i uczy się go każde dziecko. Nie powinno sprawiać większych problemów wyliczenia czasu spadania przysłowiowego newtonowskiego jabłka. Problem staje się skomplikowany, gdy obliczamy wzajemne oddziaływania pomiędzy Ziemią, a Księżycem, a praktycznie nierozwiązywalny bez użycia komputerów, gdy chcemy zbadać tę kwestię dla większej ilości obiektów kosmicznych.
Z matematycznego punktu widzenia zagadnienie również wydaje się proste: należy podwójnie zróżniczkować po czasie równanie grawitacyjne Newtona. Mając masy potrafimy wyliczyć działające siły, z nich przyspieszenia, prędkości i wreszcie położenia obiektów. Otrzymane wyniki, to znane wszystkim tzw. krzywe stożkowe (np. elipsy), po których mogą poruszać się obiekty w przestrzeni. Trzeba też zaznaczyć, że dokładność obliczeń zależy od przyjętego skoku czasowego.
To proste laboratorium grawitacyjne zostało napisane jako wstęp do dużego programu, który zostanie niebawem opisany. Zawiera mnóstwo niedoróbek i nie jest odporne na różne podawane przez użytkownika parametry. Mimo tego, przy odrobinie prób i błędów możemy:
- zasymulować ruch w polu grawitacyjnym 4 obiektów.
- podać ich masy, początkowe położenia i początkowe prędkości
- podać tzw. „skok czasowy” – jak szybko będzie upływał czas
- skalować obszar wykresu - przestrzeni kosmicznej
- zmieniać wielkość i kolor planet
Tylko dzięki takim minimalnym parametrom możemy na przykład:
- zbadać oddziaływanie Słońca, Ziemi i Księżyca
- zasymulować rzut pionowy, poziomy, ukośny i swobodny spadek na ziemi
- wystartować rakietą i „zaparkować” na orbicie ziemskiej
- przetestować prędkości kosmiczne
- obejrzeć „działanie” pulsara
- przetestować wyrzutnię grawitacyjną
- sprawdzić "dlaczego wszystko się kręci"
- i wiele, wiele innych zjawisk kosmicznych
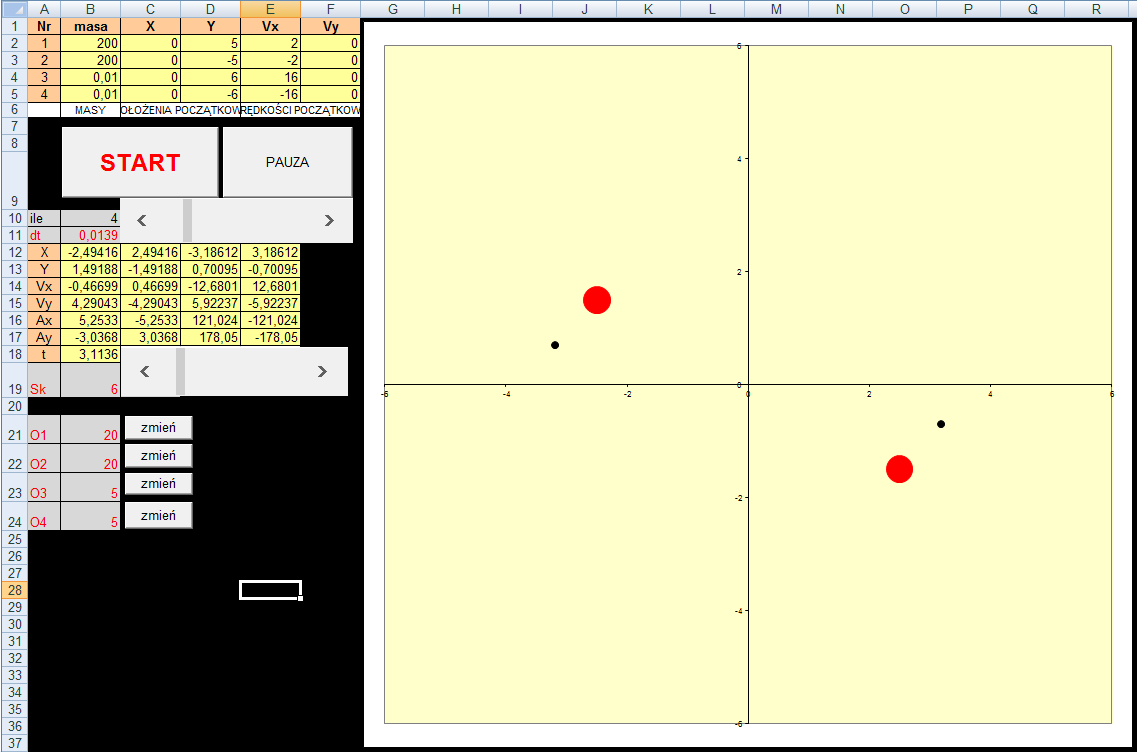
Symulacja komputerowa pulsara z księżycami:
Program nie jest zbyt skomplikowany i korzysta ze znanego ogólnie algorytmu Eulera, który wylicza podstawowe parametry poruszających się w polu grawitacyjnym obiektów w przestrzeni dwuwymiarowej.
Dla wszystkich zainteresowanych program GRAWILAB do pobrania
W tablicach przechowywane są:
RX i RY - położenia obiektów
VX i VY – prędkości obiektów
AX i AY – przyspieszenia obiektów
Public tt, dt As Double
Public koniec As Boolean
Public pauza As Boolean
Sub auto_open()
koniec = True
pauza = True
ActiveSheet.Shapes("STST").Select
Selection.Characters.Text = "START"
Range("A6").Select
End Sub
'zmiana na suwaku czasu
Sub zmianaDT()
dt = Range("B11")
End Sub
''klawisz START-STOP
Sub Obsługa()
If koniec = True Then
t = "STOP"
koniec = False
ActiveSheet.Shapes("STST").Select
Selection.Characters.Text = t
Range("A6").Select
sym3
Else
t = "START"
koniec = True
ActiveSheet.Shapes("STST").Select
Selection.Characters.Text = t
Range("A6").Select
End If
End Sub
'klawisz pauza
Sub Pauzowanie()
If pauza = True Then
pauza = False
tt = dt
dt = 0
Else
pauza = True
dt = tt
End If
End Sub
'symulacja
Sub sym3()
Const WYM = 5
Const G = 1 '6.67259E-11 'm kg s na potrzeby programu 1
Dim MA(1 To WYM) As Double
Dim XY(1 To WYM, 1 To 2) As Double
Dim VV(1 To WYM, 1 To 2) As Double
Dim AA(1 To WYM, 1 To 2) As Double
Dim i, j, k As Integer
Dim R, R2, R3, t As Double
t = 0
dt = Range("B11") '0.01
sk = Range("B19")
N = Range("B10") 'ile obiektów
'pobranie danych
For i = 1 To N
w = i + 1
MA(i) = Cells(w, 2)
XY(i, 1) = Cells(w, 3) 'X
XY(i, 2) = Cells(w, 4) 'Y
VV(i, 1) = Cells(w, 5) 'VX
VV(i, 2) = Cells(w, 6) 'VY
Next i
'pętla główna
Do
'wyzerowanie przyspieszeń
For i = 1 To N
For k = 1 To 2
AA(i, k) = 0
Next k
Next i
'obliczanie przyspieszeń
For i = 1 To N
For j = 1 To N
If i <> j Then
'odległości pomiędzy planetami
R2 = (XY(i, 1) - XY(j, 1)) ^ 2 + (XY(i, 2) - XY(j, 2)) ^ 2
R = R2 ^ (1 / 2)
R3 = R ^ 3
' suma wszystkich składowych
For k = 1 To 2
AAch = -G * MA(j) * (XY(i, k) - XY(j, k)) / R3
AA(i, k) = AA(i, k) + AAch
Next k
End If
Next j
Next i
'nowe położenia i prędkości
For i = 1 To N
For k = 1 To 2
VV(i, k) = VV(i, k) + AA(i, k) * dt
XY(i, k) = XY(i, k) + VV(i, k) * dt
Next k
Next i
'dane na ekran
t = t + dt
For i = 1 To N
w = 10
k = 1
Cells(w + 2, k + i) = XY(i, 1)
Cells(w + 3, k + i) = XY(i, 2)
Cells(w + 4, k + i) = VV(i, 1)
Cells(w + 5, k + i) = VV(i, 2)
Cells(w + 6, k + i) = AA(i, 1)
Cells(w + 7, k + i) = AA(i, 2)
Cells(w + 8, k + 1) = t
Next i
'po kalkulacji zmienia się wykres
Calculate
DoEvents
Loop Until koniec Or Abs(XY(1, 1)) > 2 * sk Or Abs(XY(1, 1)) > 2 * sk Or Abs(XY(2, 1)) > 2 * sk Or Abs(XY(2, 2)) > 2 * sk
End Sub
Sub skalaeuler()
s = Range("B19")
ActiveSheet.ChartObjects("Wykres 1").Activate
ActiveChart.Axes(xlCategory).Select
With ActiveChart.Axes(xlCategory)
.MinimumScale = -s
.MaximumScale = s
End With
ActiveChart.Axes(xlValue).Select
With ActiveChart.Axes(xlValue)
.MinimumScale = -s
.MaximumScale = s
End With
Range("A6").Select
End Sub
Sub Obiekt1()
s = Range("B21")
ActiveSheet.ChartObjects(1).Activate
ActiveChart.SeriesCollection(1).Select
ActiveChart.SeriesCollection(1).Points(1).Select
Selection.MarkerSize = s
Range("A6").Select
End Sub
Sub Obiekt2()
s = Range("B22")
ActiveSheet.ChartObjects(1).Activate
ActiveChart.SeriesCollection(1).Select
ActiveChart.SeriesCollection(1).Points(2).Select
Selection.MarkerSize = s
Range("A6").Select
End Sub
Sub Obiekt3()
s = Range("B23")
ActiveSheet.ChartObjects(1).Activate
ActiveChart.SeriesCollection(1).Select
ActiveChart.SeriesCollection(1).Points(3).Select
Selection.MarkerSize = s
Range("A6").Select
End Sub
Sub Obiekt4()
s = Range("B24")
ActiveSheet.ChartObjects(1).Activate
ActiveChart.SeriesCollection(1).Select
ActiveChart.SeriesCollection(1).Points(4).Select
Selection.MarkerSize = s
Range("A6").Select
End Sub
